私は2024年1月3日現在、AI機械学習フレームワークとしてPyTorchを利用し、Deep Convolutional Neural Network (DCNN)のモデルをディープ ラーニングにより学習させて画像処理、会社で画像検査システムの製作などをしております。
各種オプティマイザーの挙動のプロットの例 1
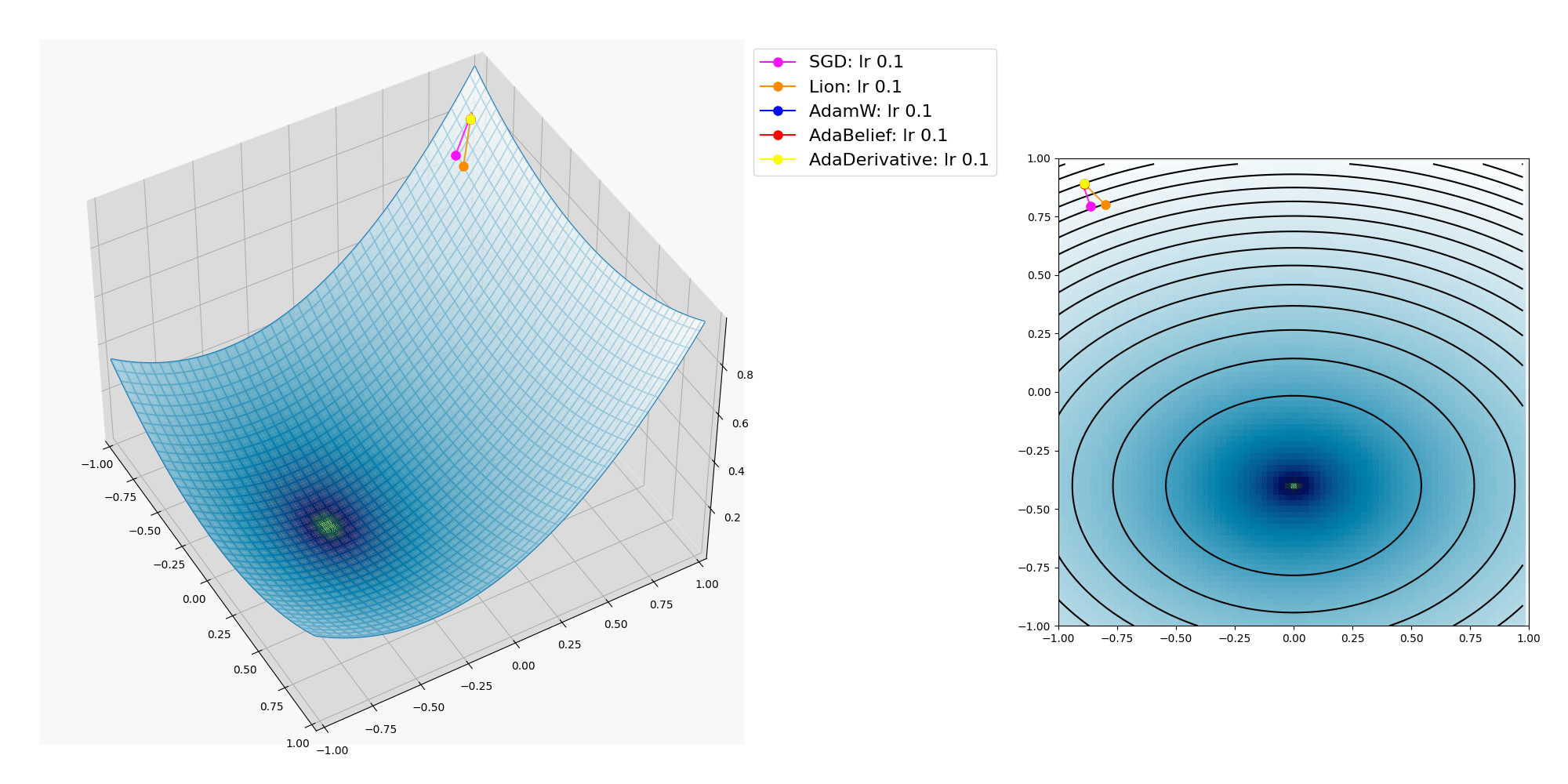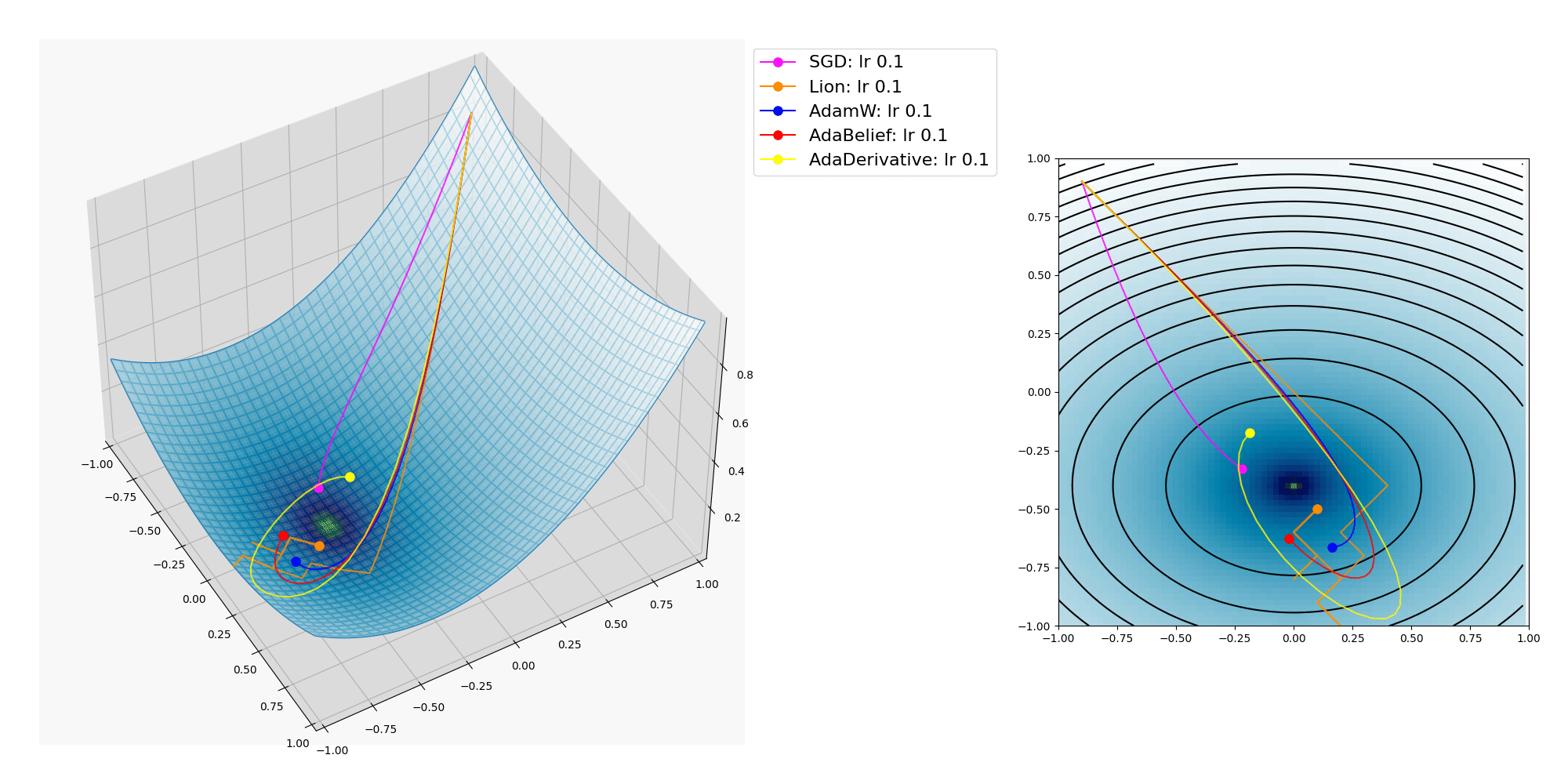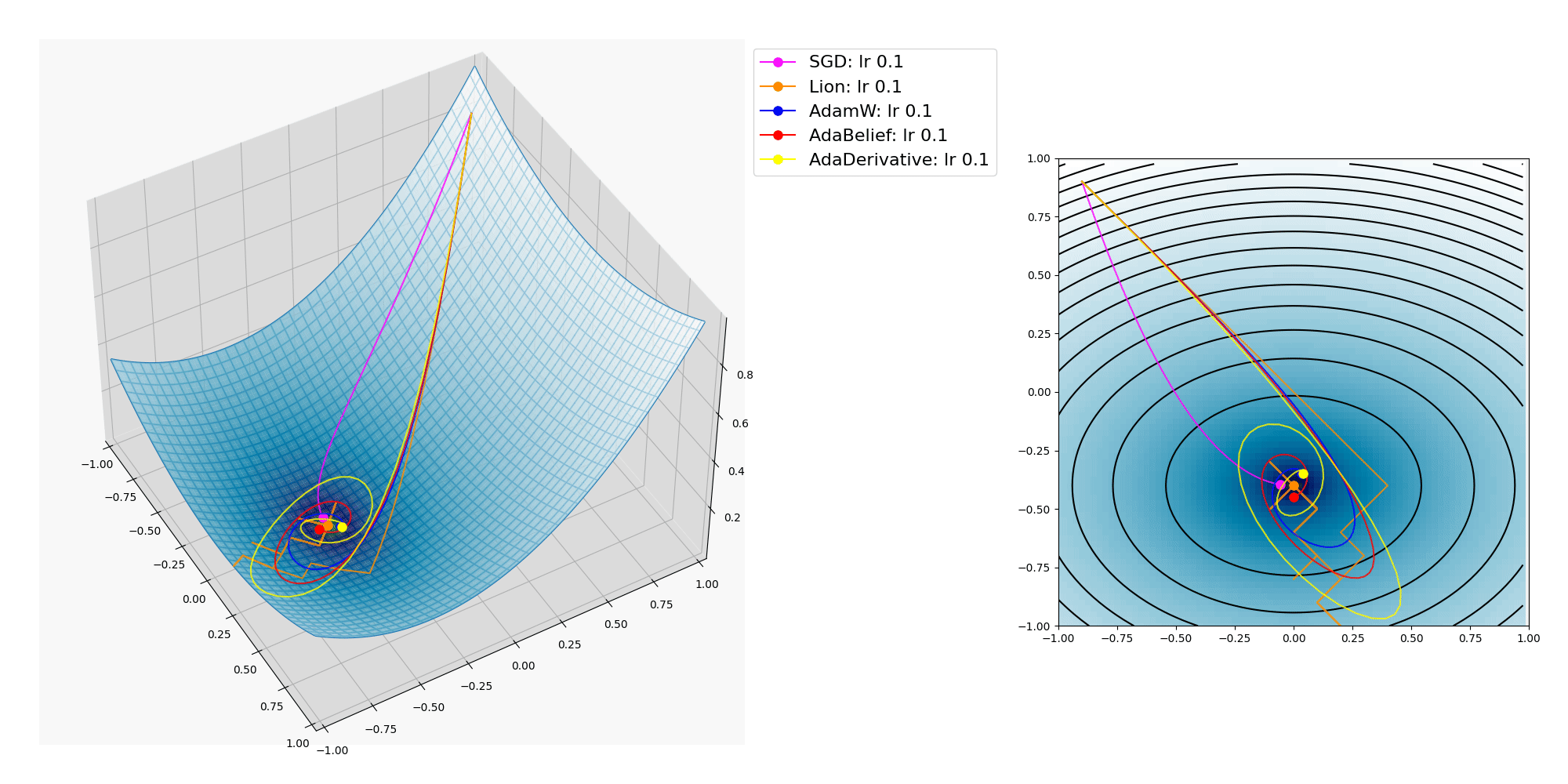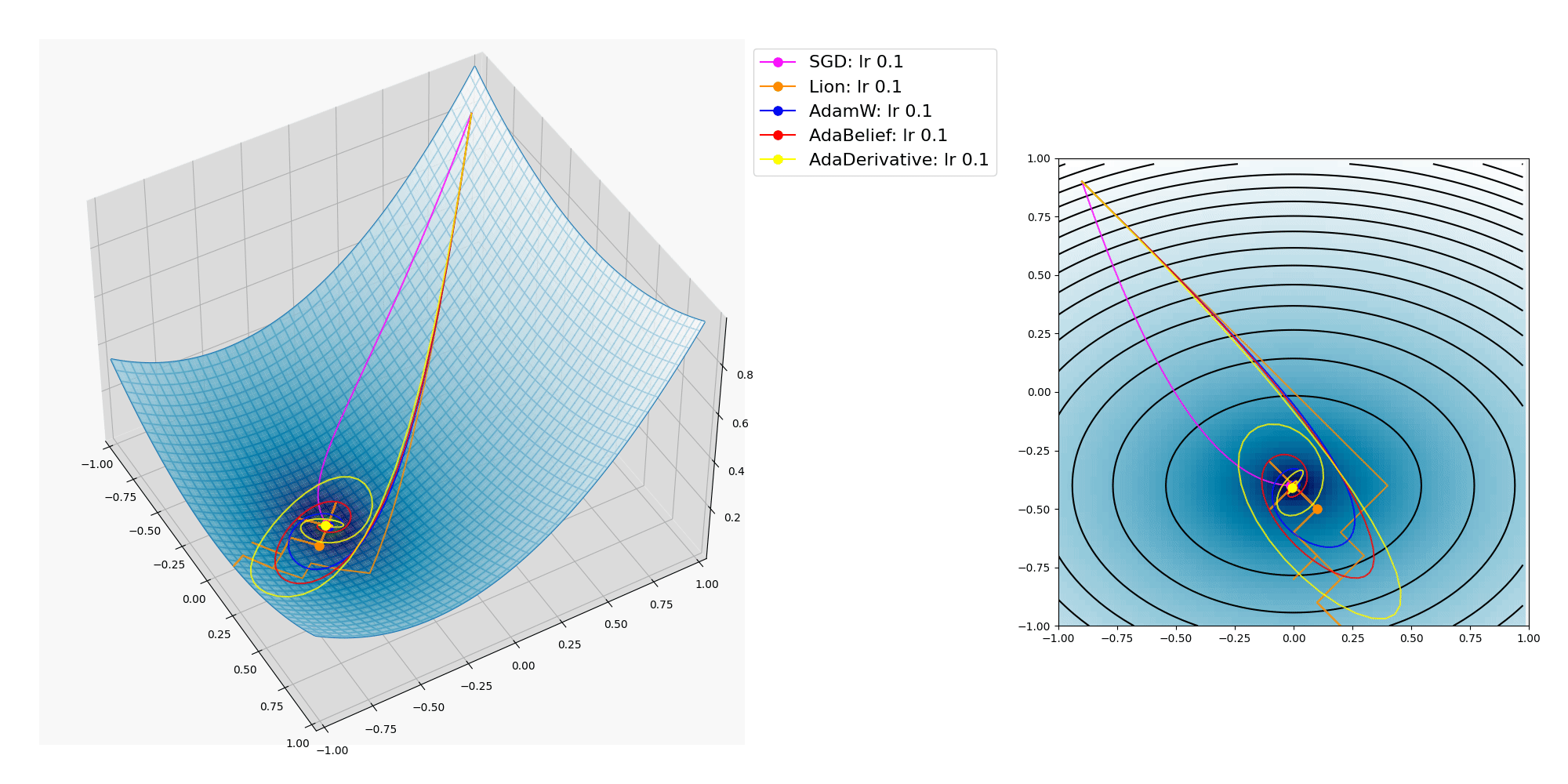
ここにオプティマイザーの振る舞いをMatplotlibで3Dグラフにプロットして視覚化した図を掲載します。
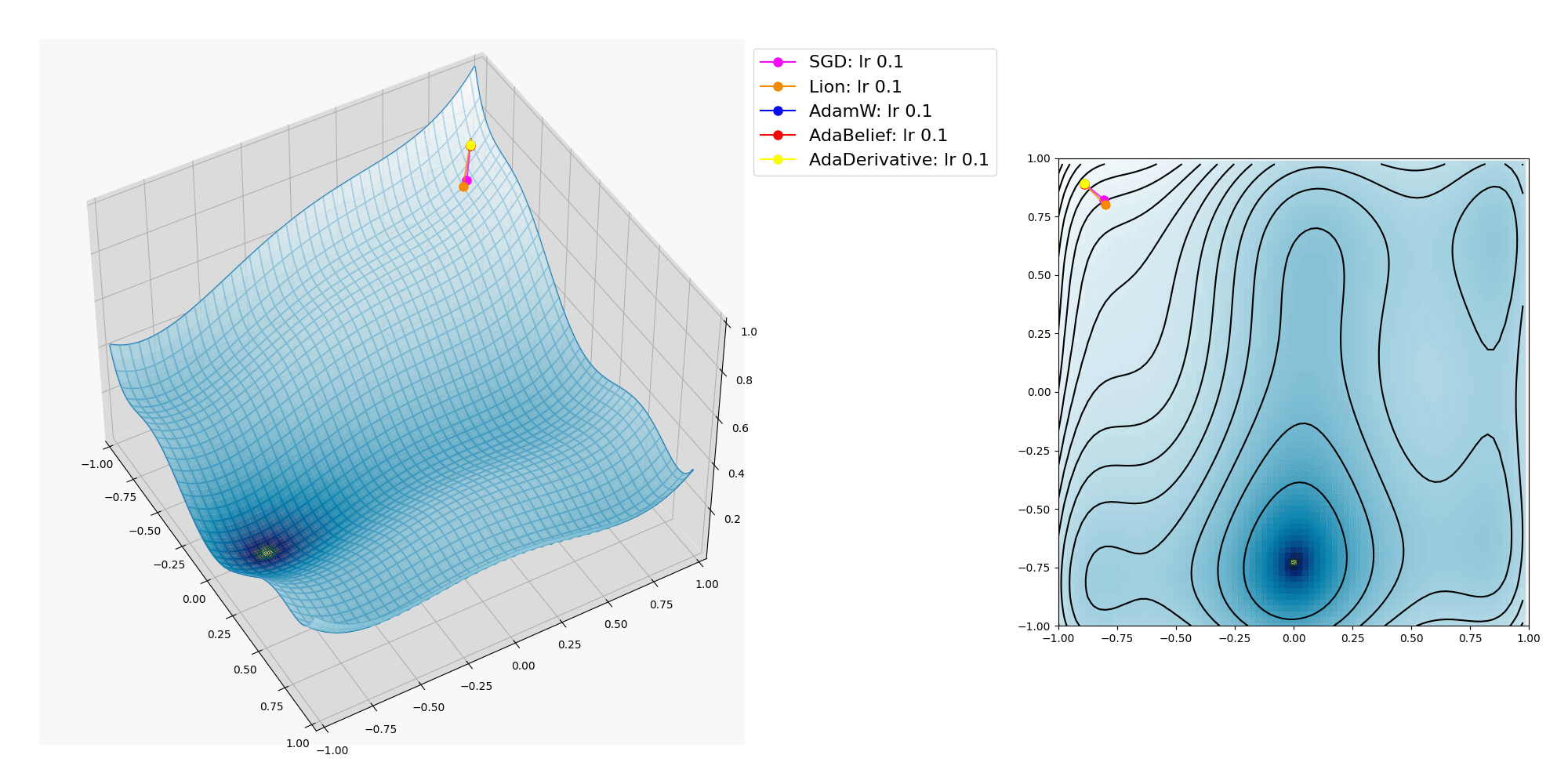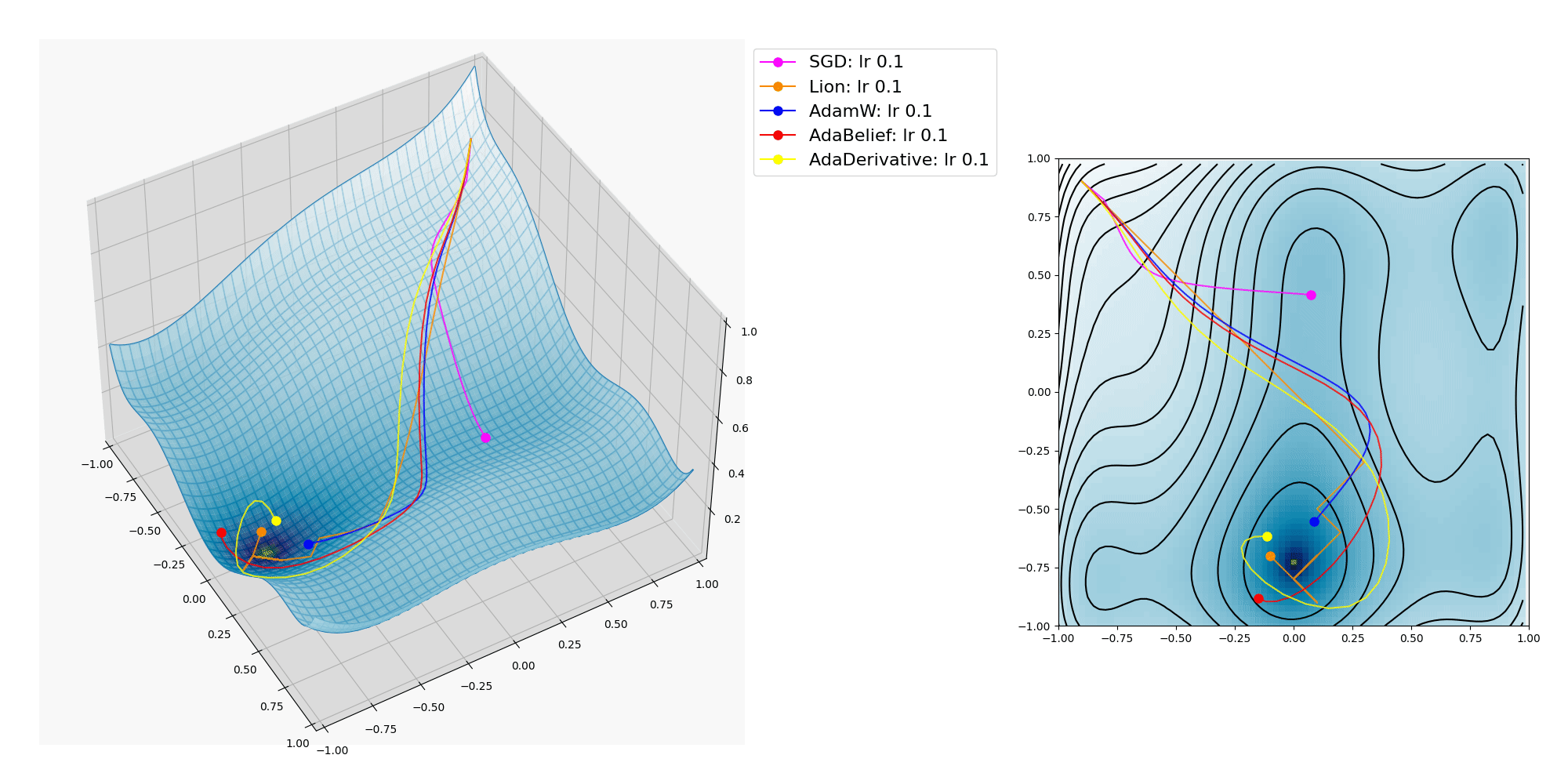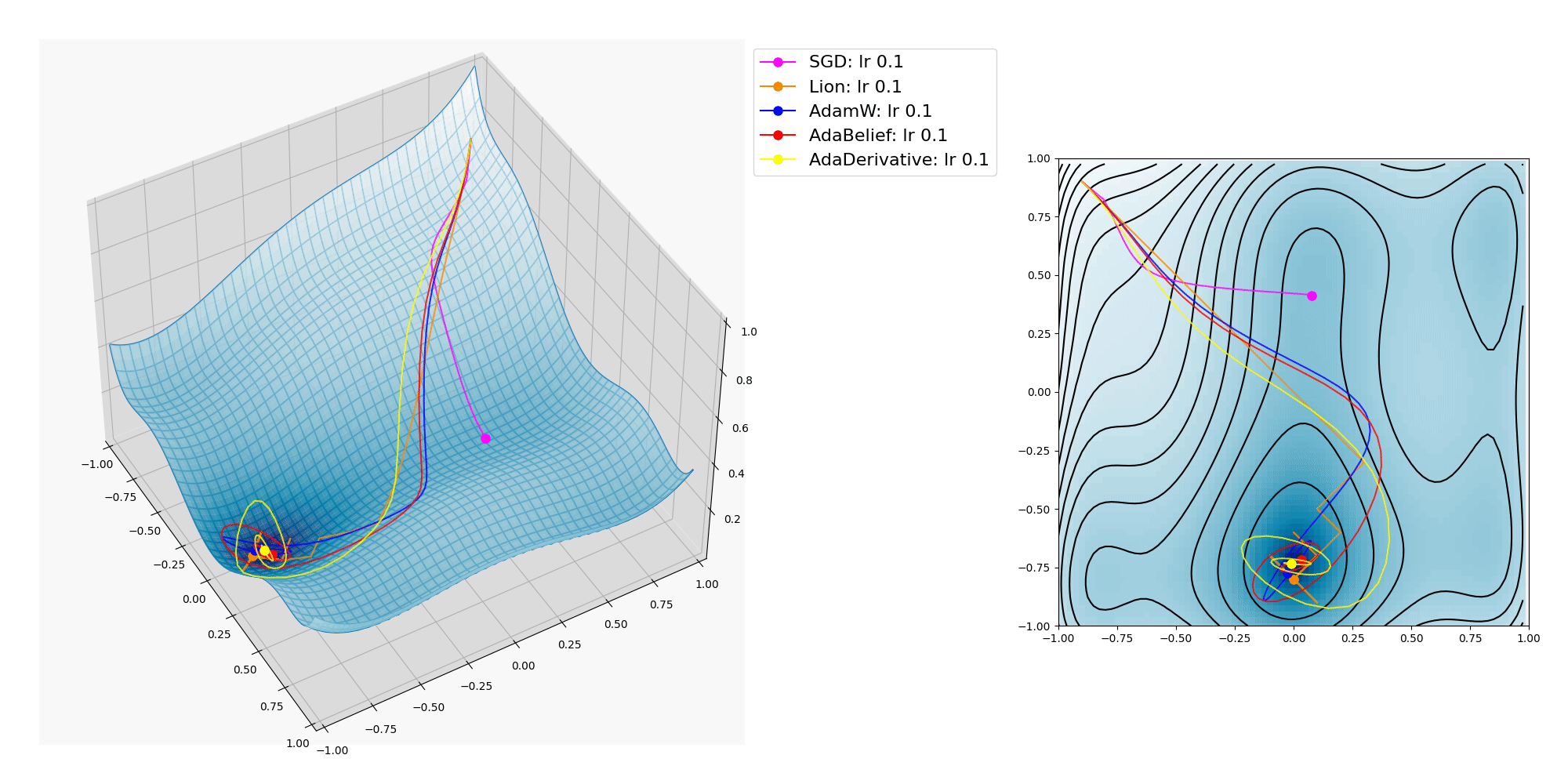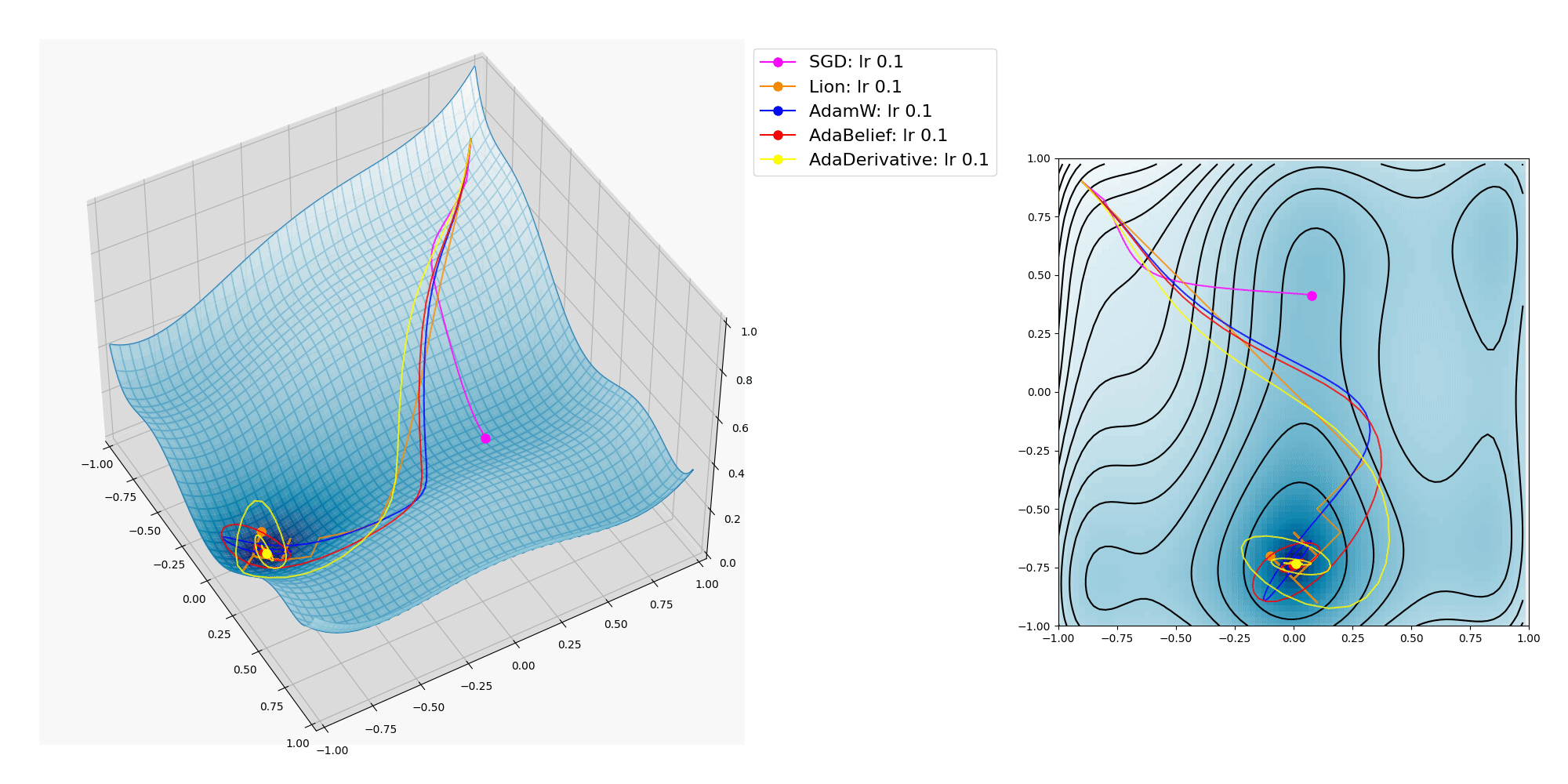
SGD, Lion, AdamW, AdaBelief, AdaDerivative の各種オプティマイザーについて。
各種オプティマイザーが x, y の2つのパラメーターを逐次変化させて目的関数の大域的最適解(極小値であり最小値 / global minima, 最も低い地点)への到達を目指します。
上記プロットでは Lion, AdamW, AdaBelief, AdaDerivativeは大域的最適解に到達出来ていますが、 SGD は局所的最適解(最小ではない極小値 / local minima)に嵌ってしまいました。
オプティマイザーについて
以下、オプティマイザーについての簡単な説明です。
機械学習フレームワークでは、まずモデルのネットワークを合成関数として計算グラフ化し、これに何らかのデータを入力して順伝播させます。
ネットワーク内を伝播する情報は、非線形の活性化関数でその一部が切り捨てられる事で加工され洗練されて行きます。
そしてモデルからの出力と所望の出力との誤差を得ます。
次に、順伝播時に記録されたパラメーターの勾配情報に基づいて微分の連鎖律を利用した自動微分機能で誤差を逆伝播してパラメーターを目的に適うように更新して最適化して行きます。
この手法を誤差逆伝播法と言います。
この際、勾配情報からどのようにノードの重み(畳み込みのカーネルの値など)とバイアスのパラメーターを更新するのかという方策を決めるのがオプティマイザーの役割となります。
各種オプティマイザーの挙動のプロットの例 2
オプティマイザーは歴史と共に様々な種類のものが開発されて来ました。
そして私達は悩むのです。
どのオプティマイザーが良いのかと。
普通はバランスの良いAdam (Adaptive Moment Estimation / 適応的モーメント推定)を利用するでしょう。
しかしより良い結果が出るオプティマイザーがあるならば利用せずには居られません。
片っ端から試したいところですが、機械学習には高性能なPCを利用してもかなりの時間が掛かります。
実際の各オプティマイザーの振る舞いを理解する為、Python, PyTorch, Matplotlibにてこれをアニメーション グラフの図にプロットして視覚化する事にしました。
他の方々が既に沢山やって来た事の真似です。
幾つもの関数で、掲載したプロットには無いものも含めて多数のオプティマイザーを試してみた結果としては、 “AdamW” と、 “AdaBelief” 、 “AdaDerivative” が優れているようでした。
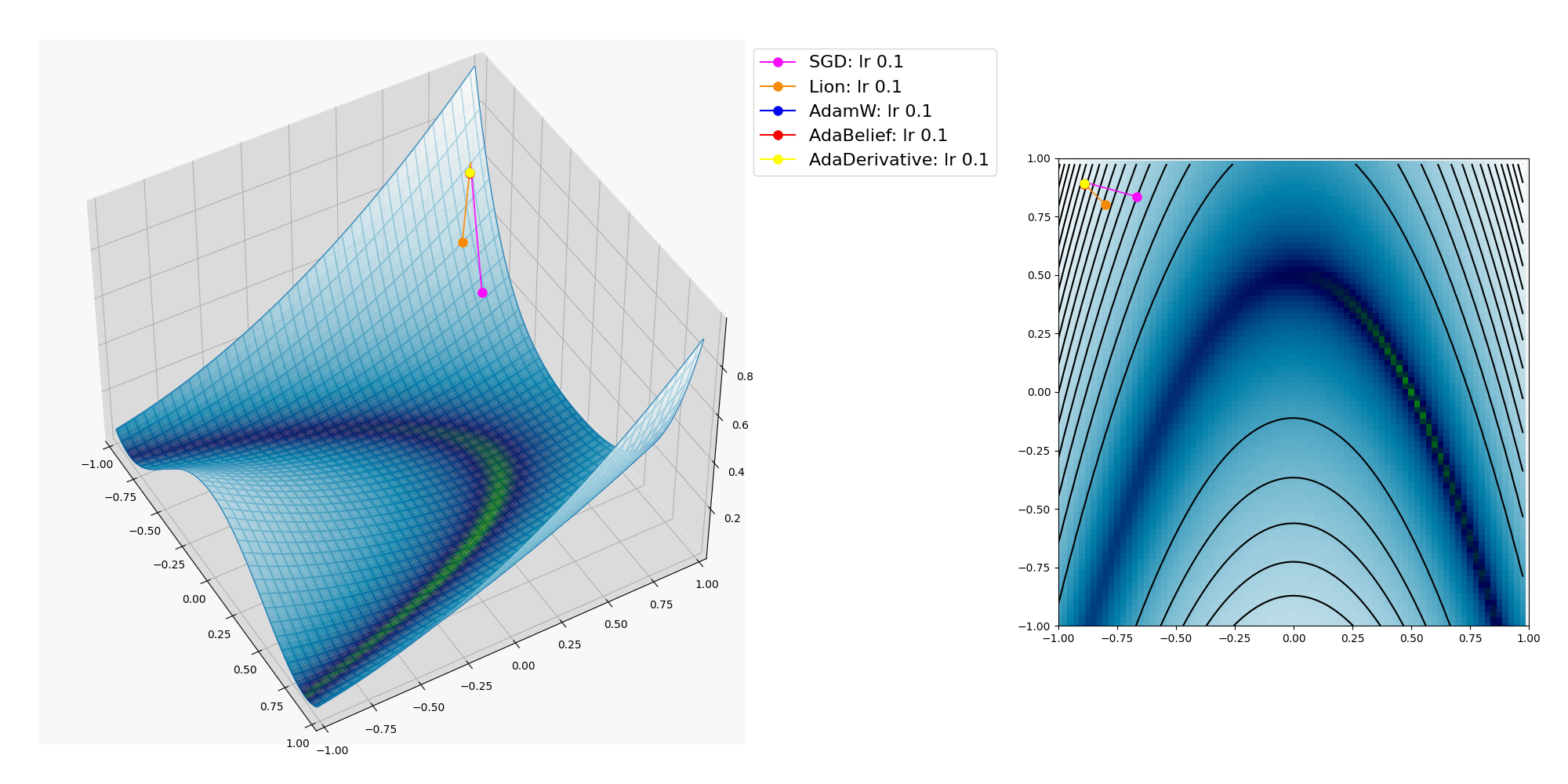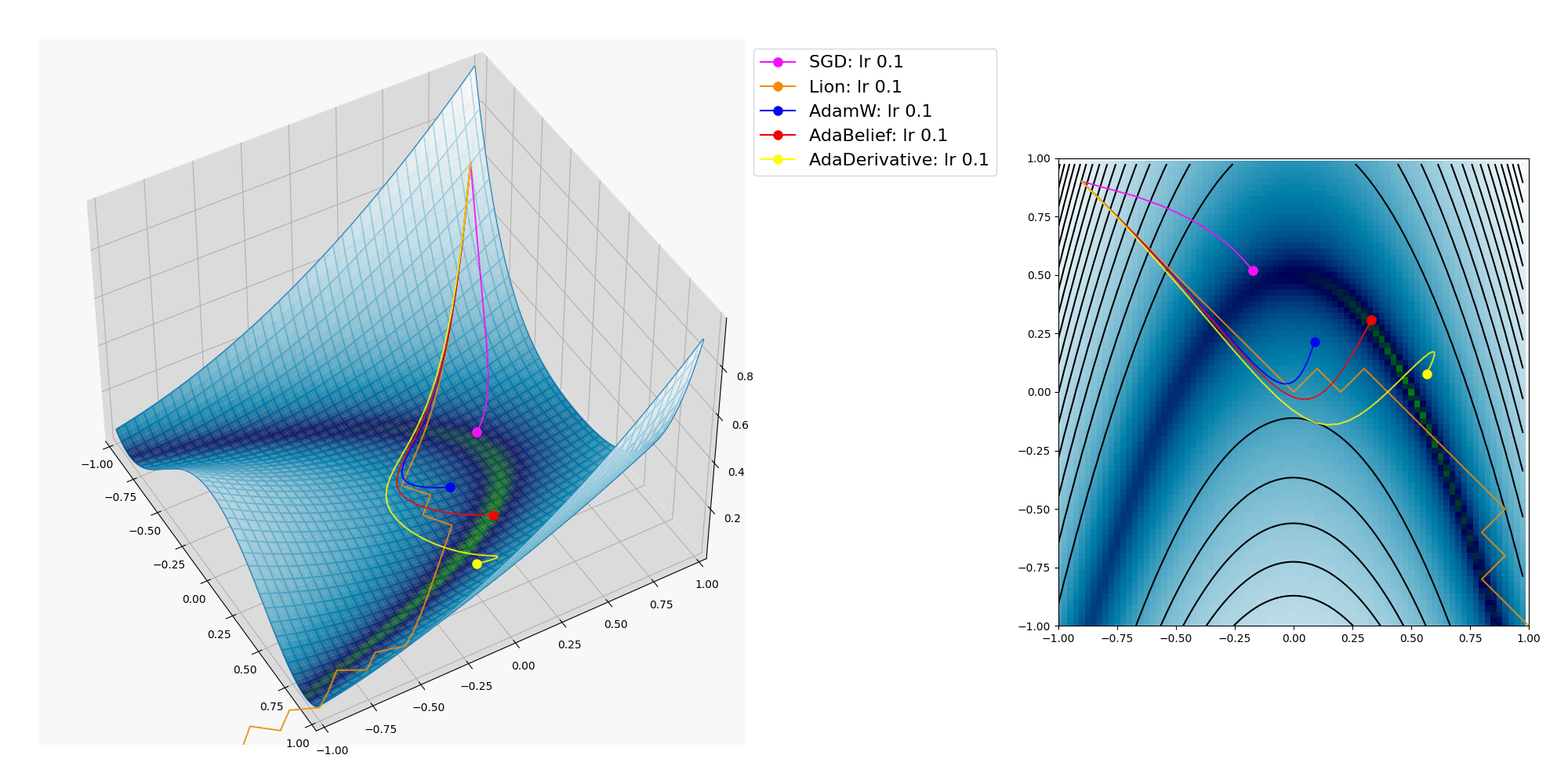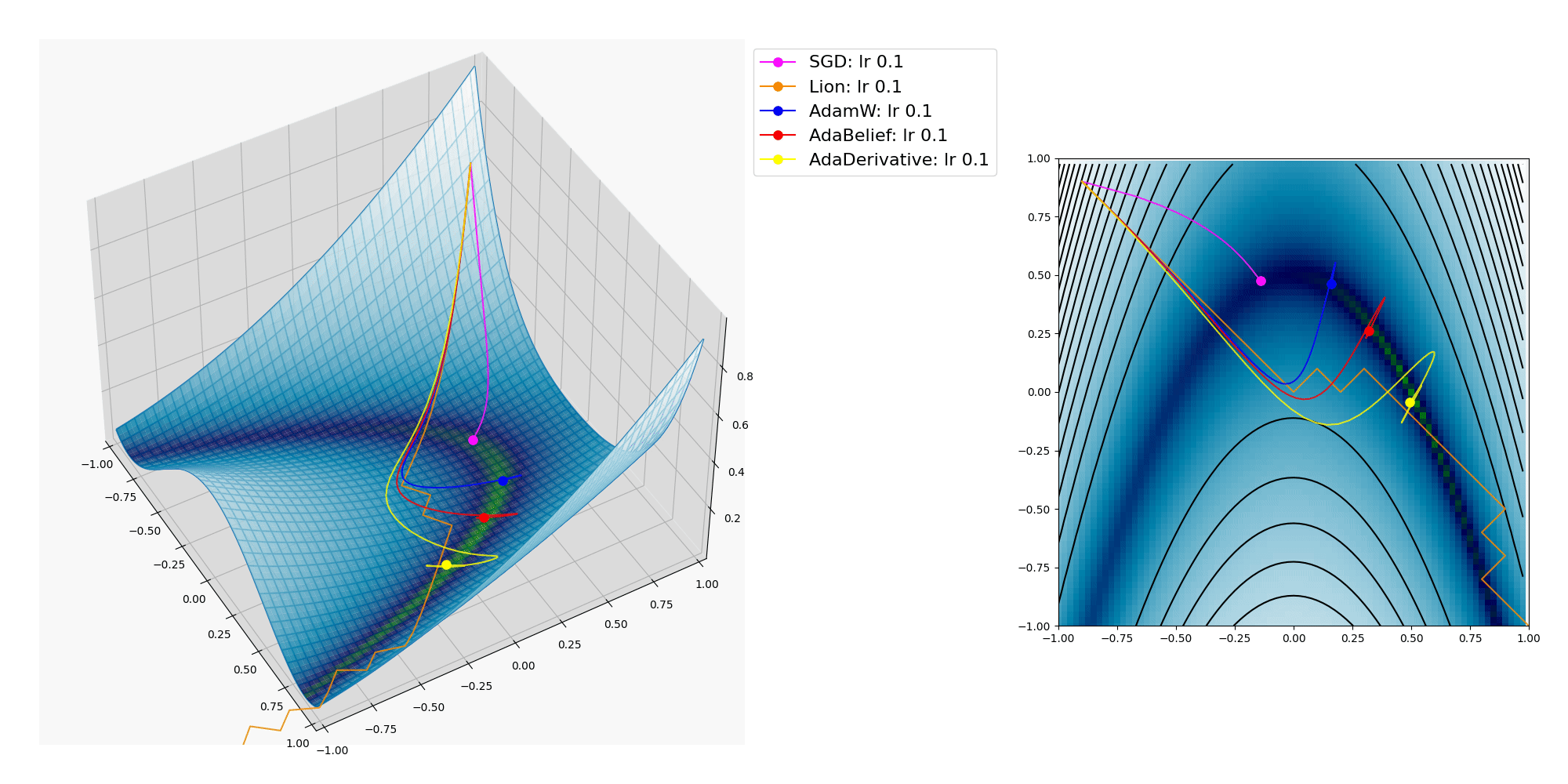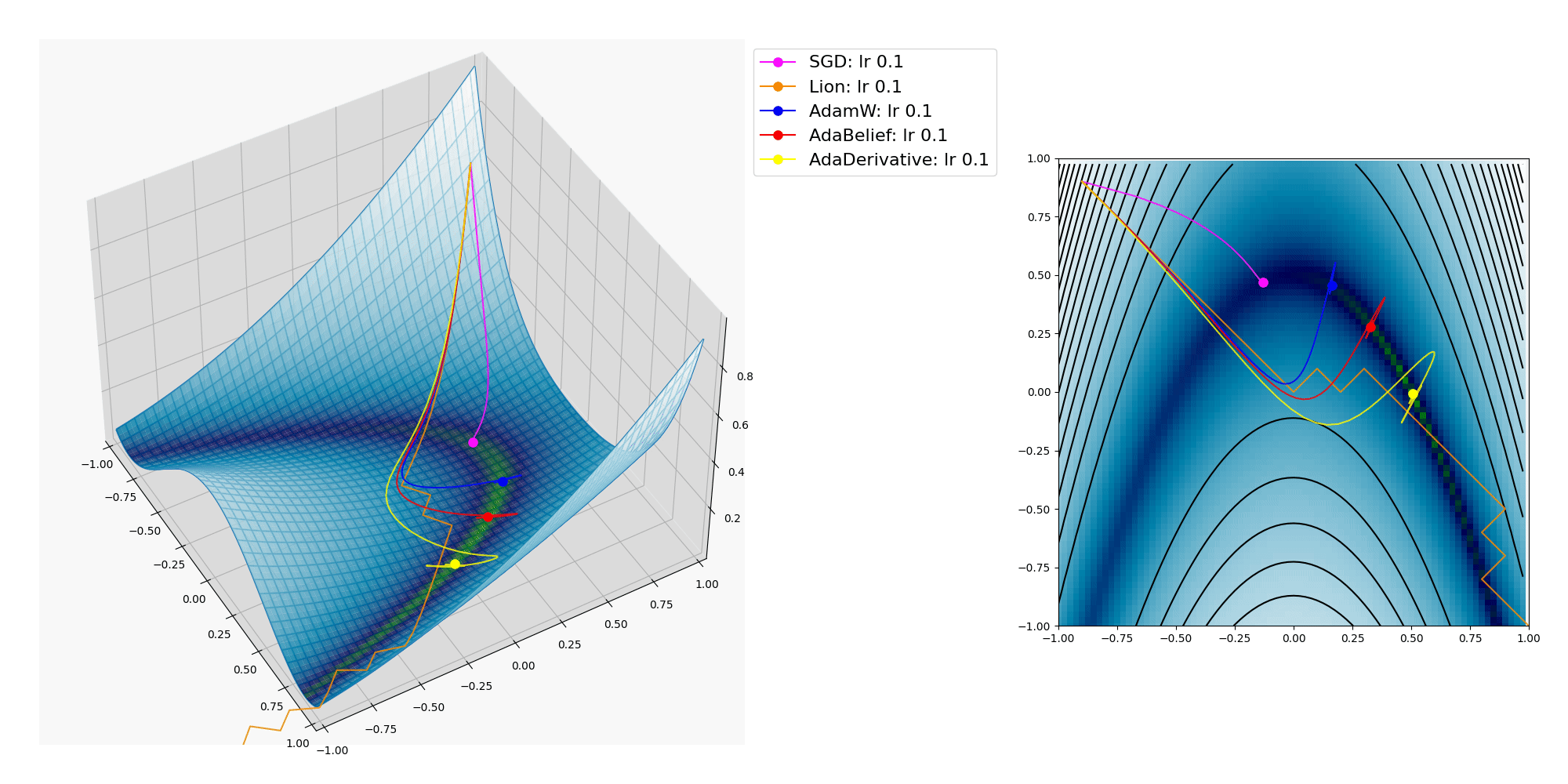
Lionは1匹だけで遠くへ行ってしまいましたね。
Lionオプティマイザーはステップ サイズが一定で、加速減速は無く、正負の符号だけが更新されます。
その為、学習率をスケジューラーなどで巧く調整してあげれば局所的最適解に嵌まらず素早く大域的最適解に到達出来る可能性は有ります。
そこそこ加速出来て余りオーヴァーシュートせず、バランスが良いのはAdaBeliefオプティマイザーでしょうか。
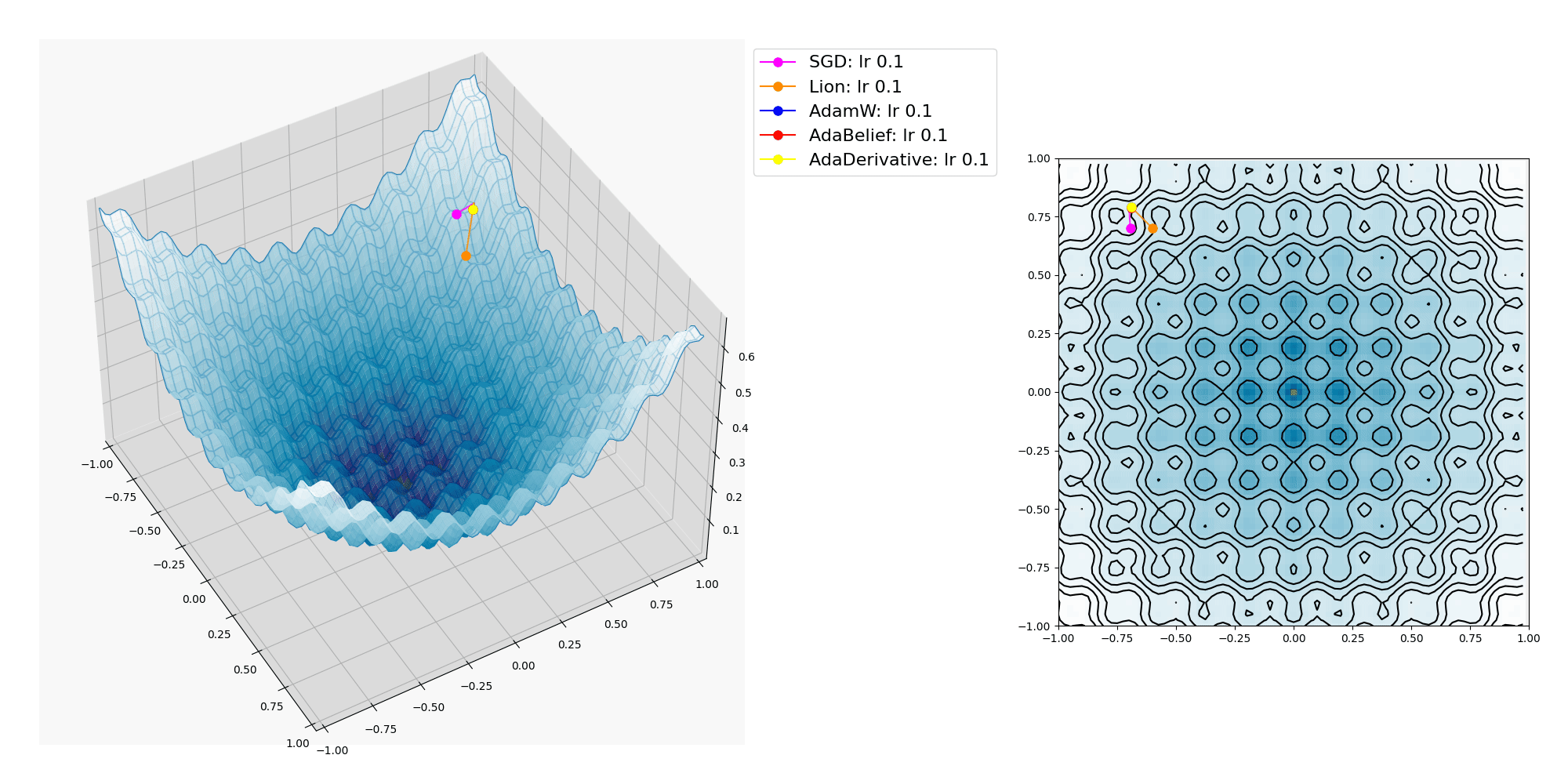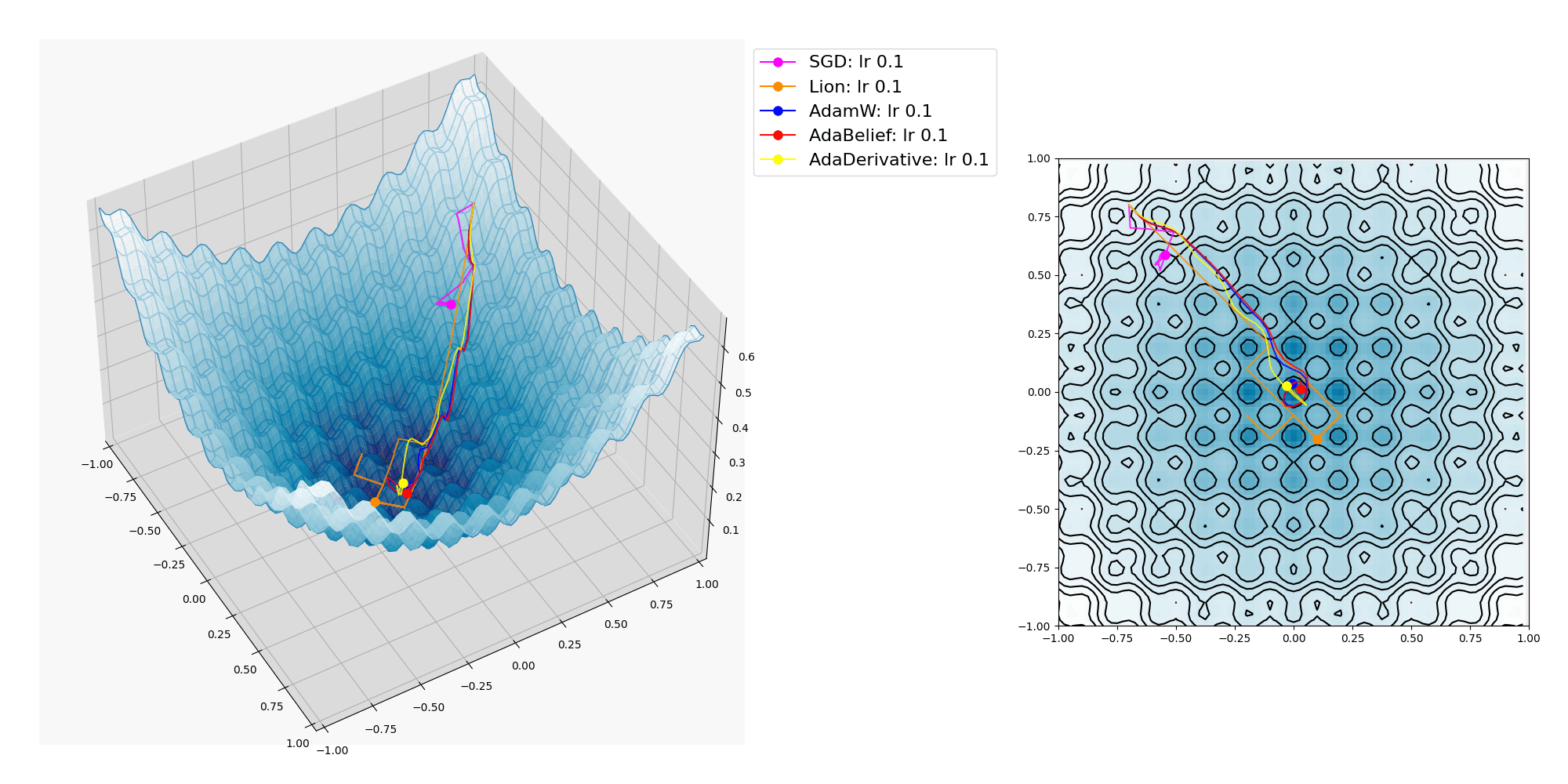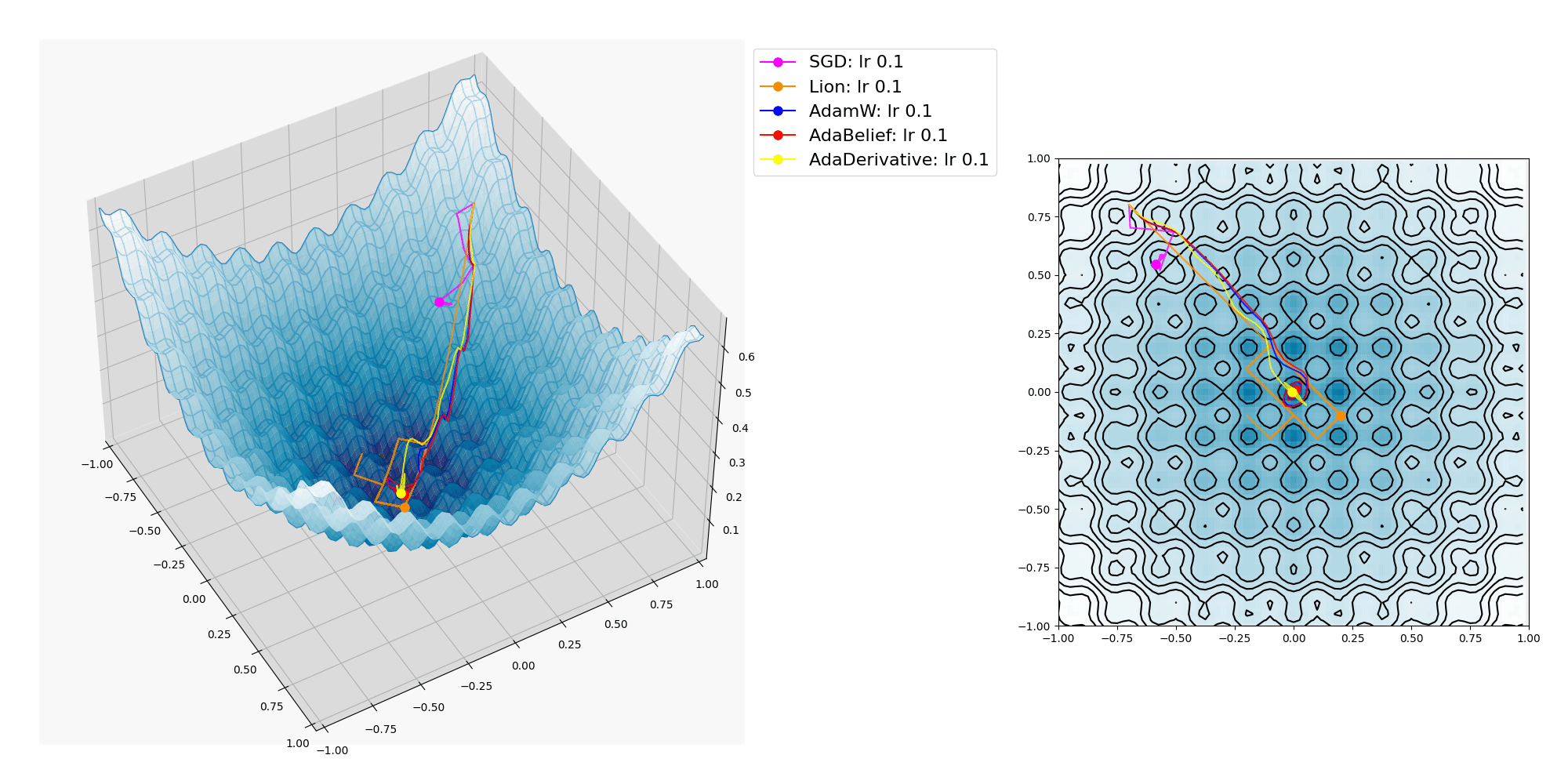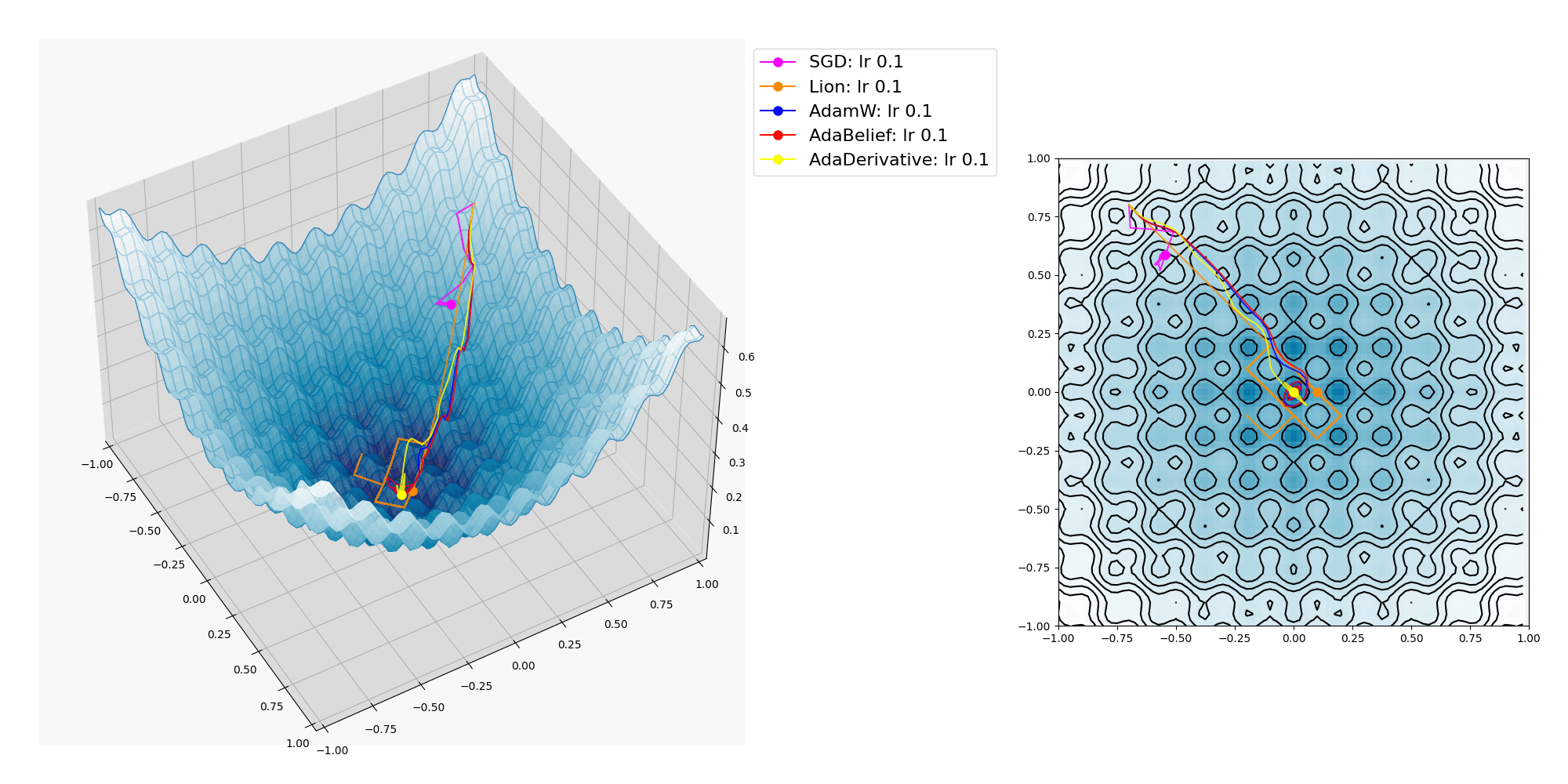
多峰性である Rastrigin関数上を各種オプティマイザーで探索させてみたところ、これは他の比較的滑らかな曲面上と異なり、学習率が小さいとほとんどの場合に局所最適解(local minima)に嵌って抜け出せなくなり、逆に学習率が大きいと曲面上を x, y パラメーターが暴れまわってどこかへ飛んで行ってしまいました。
人力で学習率の適切な値を見付けるのに苦労しました。
AdaBelief オプティマイザー
AdaBelief はBelief(信念)によって波に翻弄される事無く大域的最適解に向かう性質が有ります。
このBeliefはMomentum(慣性, 勢いvector)として働く勾配のEMA(Exponential Moving Average / 指数移動平均)を指針とし、現在の勾配の値との差を取り、これをRMSE(Root Mean Square Error / 誤差二乗平均平方根)として学習率の補正の分母に使用するようです。
この仕組みにより、勾配の偏差(平均との差)が大きな場合は学習率が下がり、偏差が小さい場合は勢い良く進む事が出来ます。
詳しくはAdaBelief Optimizerの論文著者のページを御覧下さい。
https://juntang-zhuang.github.io/adabelief/
Ubuntu PCにTeX LiveとTexmakerをインストールして簡単な疑似コードでAdaBeliefの更新式を書いてみました。
元の論文の式とは記号や式が異なっておりますので御注意の上、元の論文を御確認下さい。

AdaBC オプティマイザー(AdaBeliefの一部改変)
2024年1月3日現在、私はResidual in Residual構造のDeep Convolutional Neural Network(DCNN)を試すなどしています。
しかし、residual blockについて480ch, 128段, 256層くらいに増やしてモデル サイズを大きくし、パラメーター数を増大させると、たとえResidual in Residual構造で勾配が伝播し易くても学習が巧く進まなくなって来ます。
そこで私は元々のAdaBeliefオプティマイザーを一部改変する事により、その様な大きなモデルでも学習出来るようにしました。
元のAdam系のオプティマイザーは上記疑似コードの様に1次と2次のEMAの両方にBias Correctionが適用されていますが、AdamD論文(https://arxiv.org/abs/2110.10828)と同様に、1次のEMAのバイアス補正を削除する事により初期ステップでの学習率を小さな値から緩やかに増大させるようにしてウォームアップにしています。
加えて、AdaBoundオプティマイザーが作られた理由でもありますが、学習率は大きくなり過ぎても小さくなり過ぎても良くないとの事ですので、momentumの下限を0.1、上限を2.0にclippingする事により学習の安定性を高めています。


1次のバイアス補正を削除したAdaBeliefと、それにClippingを施したAdaBCの挙動を比べると、最適解付近で学習率が下がって来たところからLionオプティマイザーの様に角ばった動きになって来ますが差は僅かです。
尚、AdaBCはLion同様にパラメーターの更新幅に下限が有るので止まる事は有りません。
因みに、AdaBiliefの計算式のEMAをDEMA(Double EMA)やTEMA(Triple EMA)に変えたりしてみたところ、滑らかな曲面上での挙動は最良でしたが、多峰性のRastrigin関数曲面上では暴れるか局所的最適解に嵌るかしてしまい、具合が良くありませんでした。
各種オプティマイザーの挙動のプロットの例 3
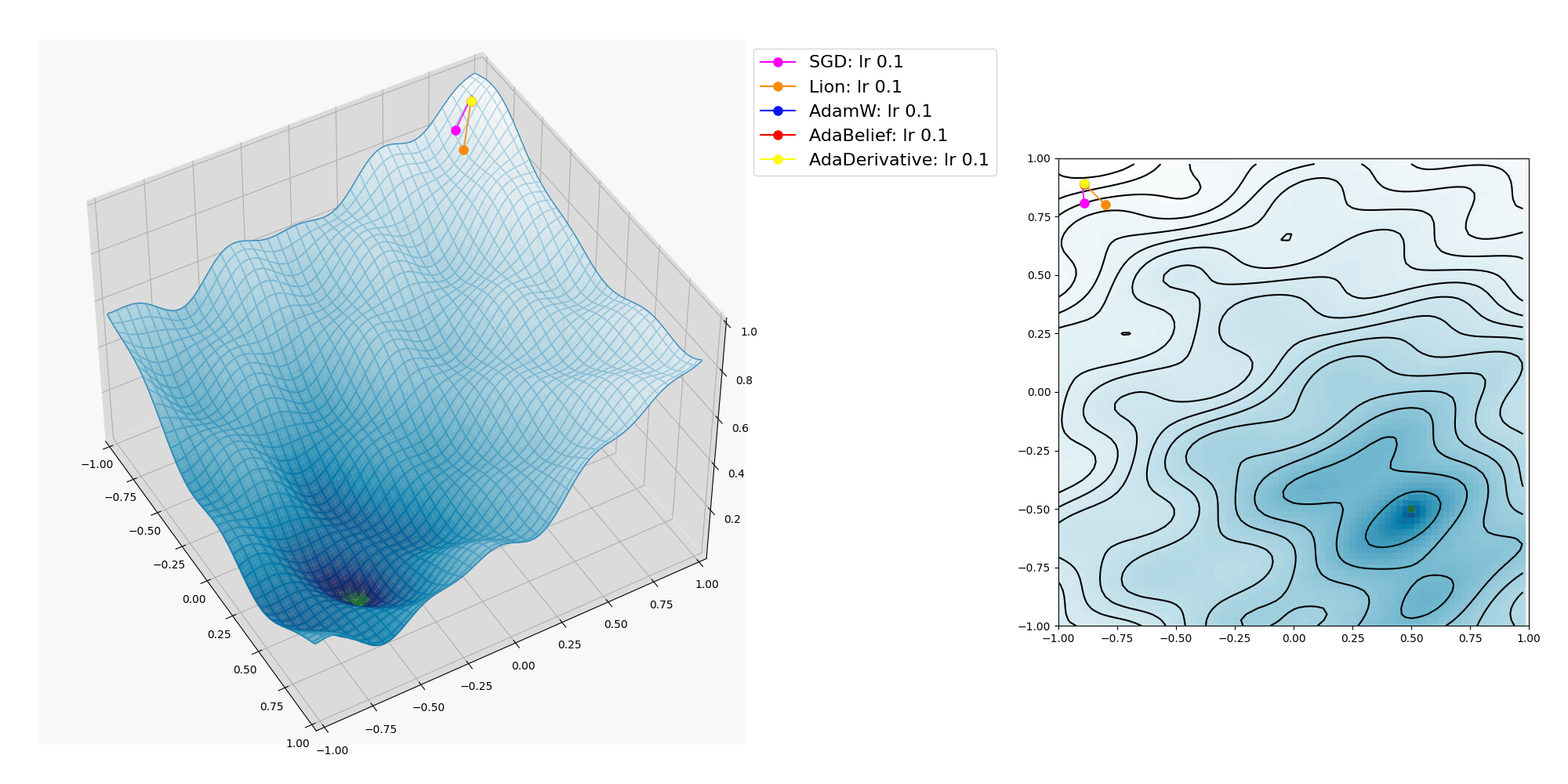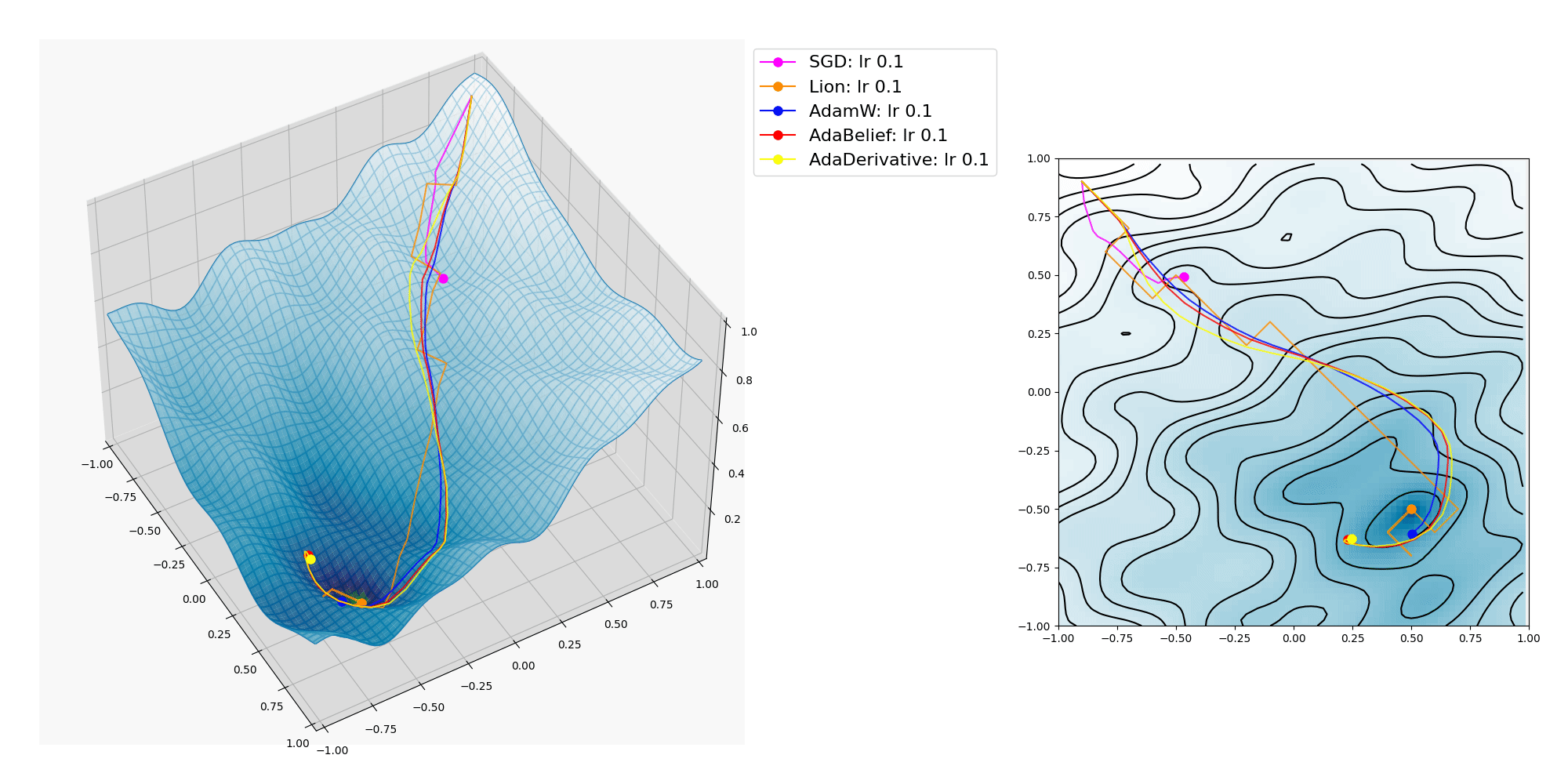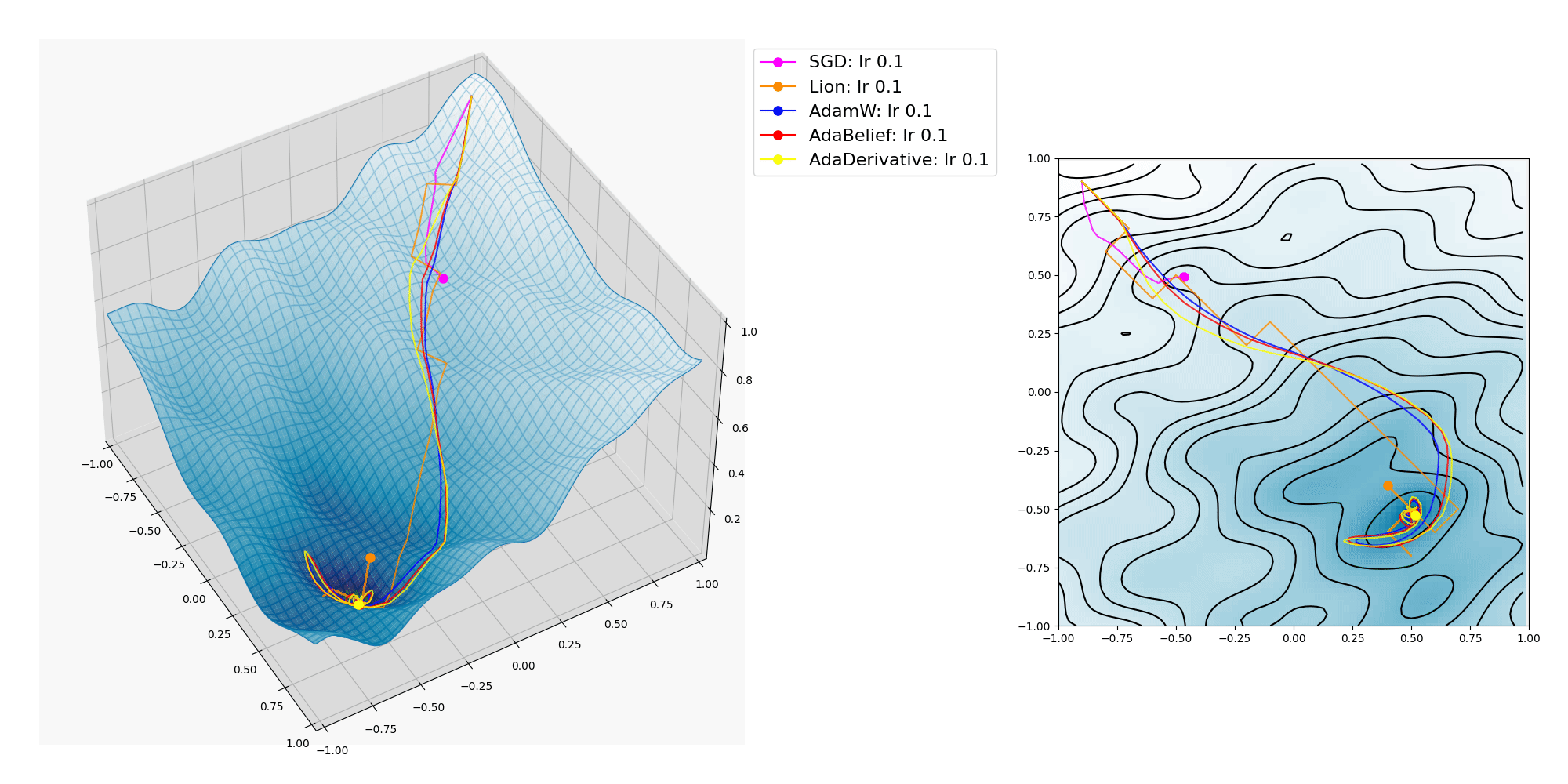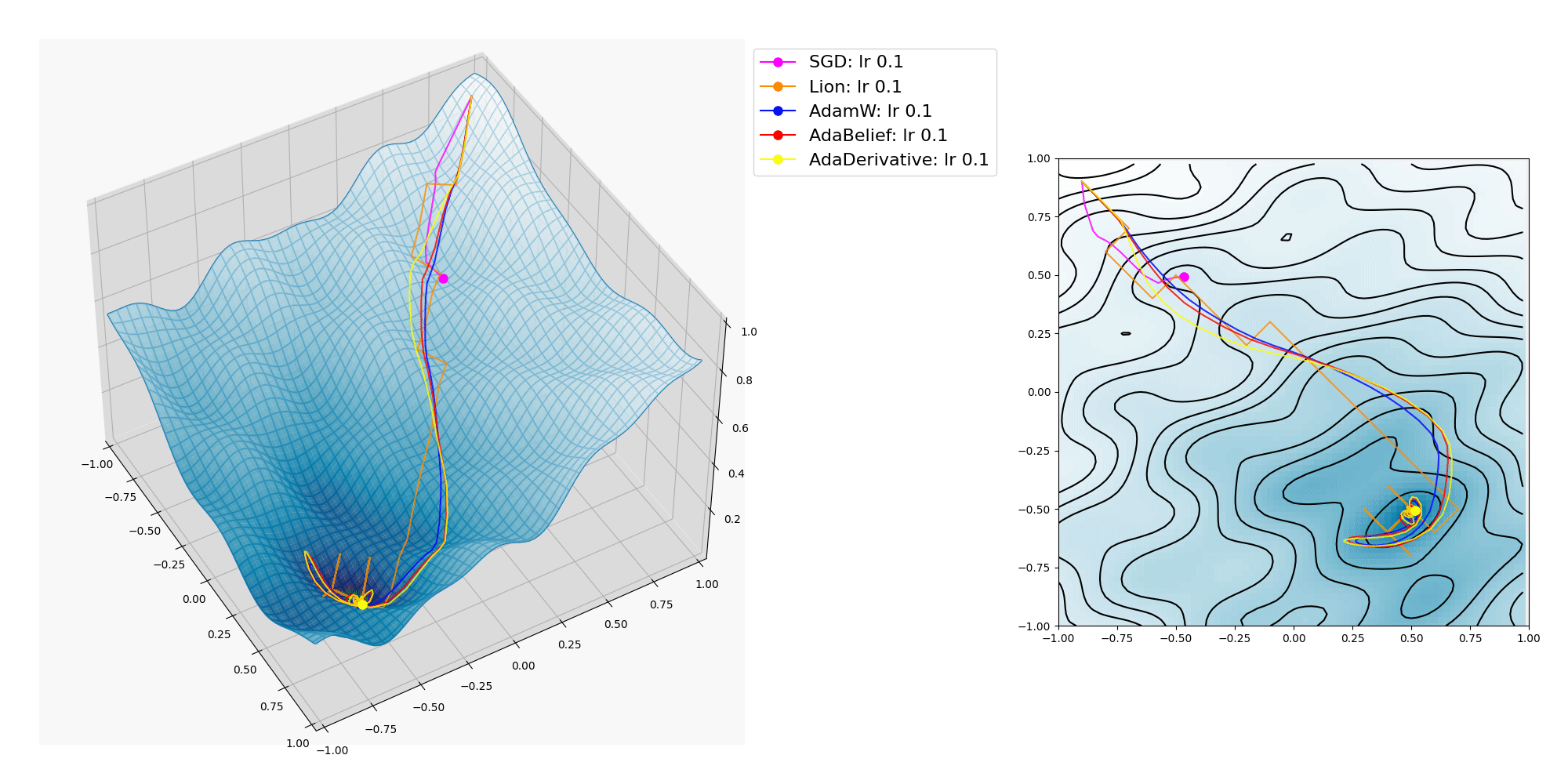
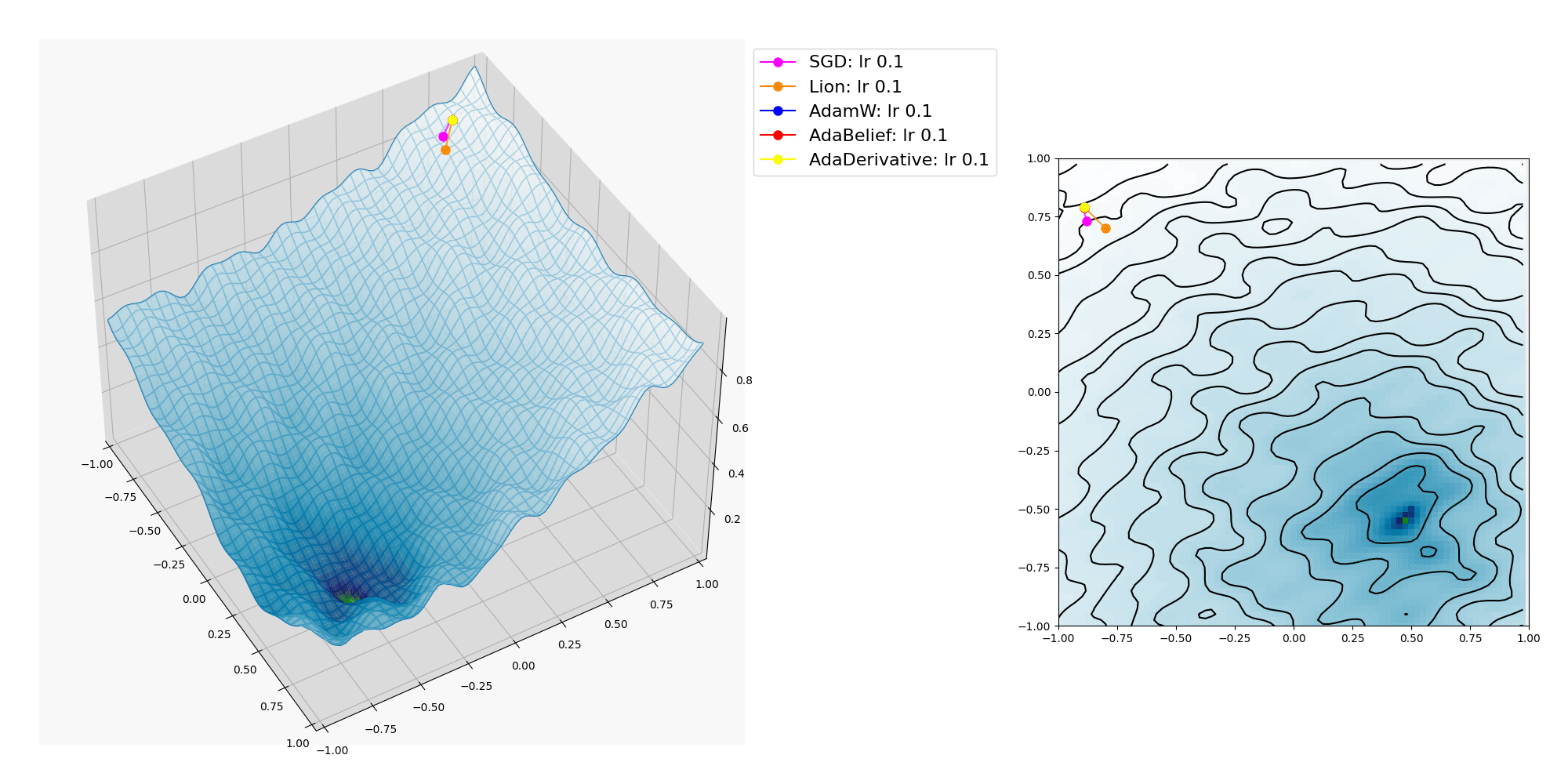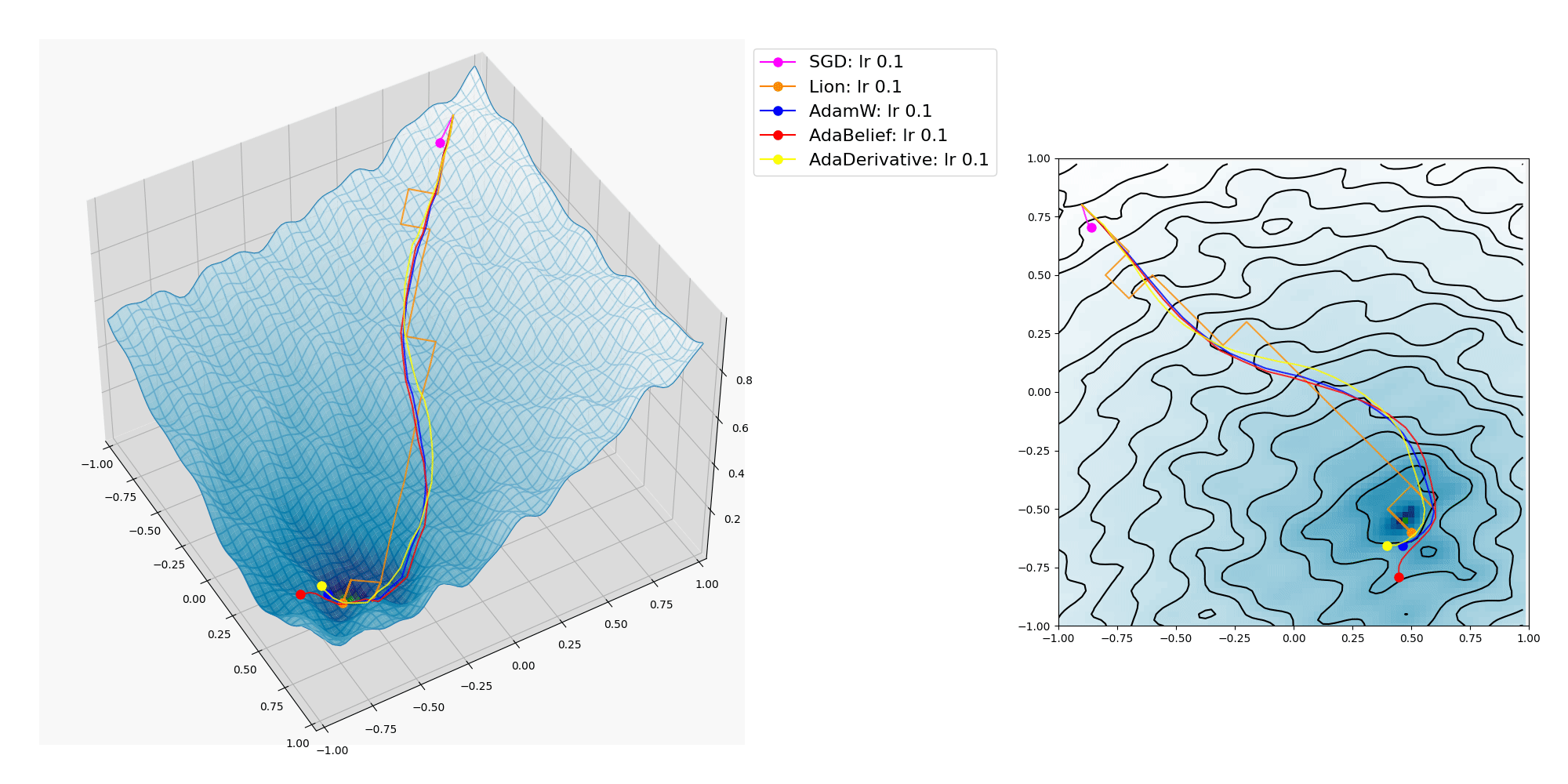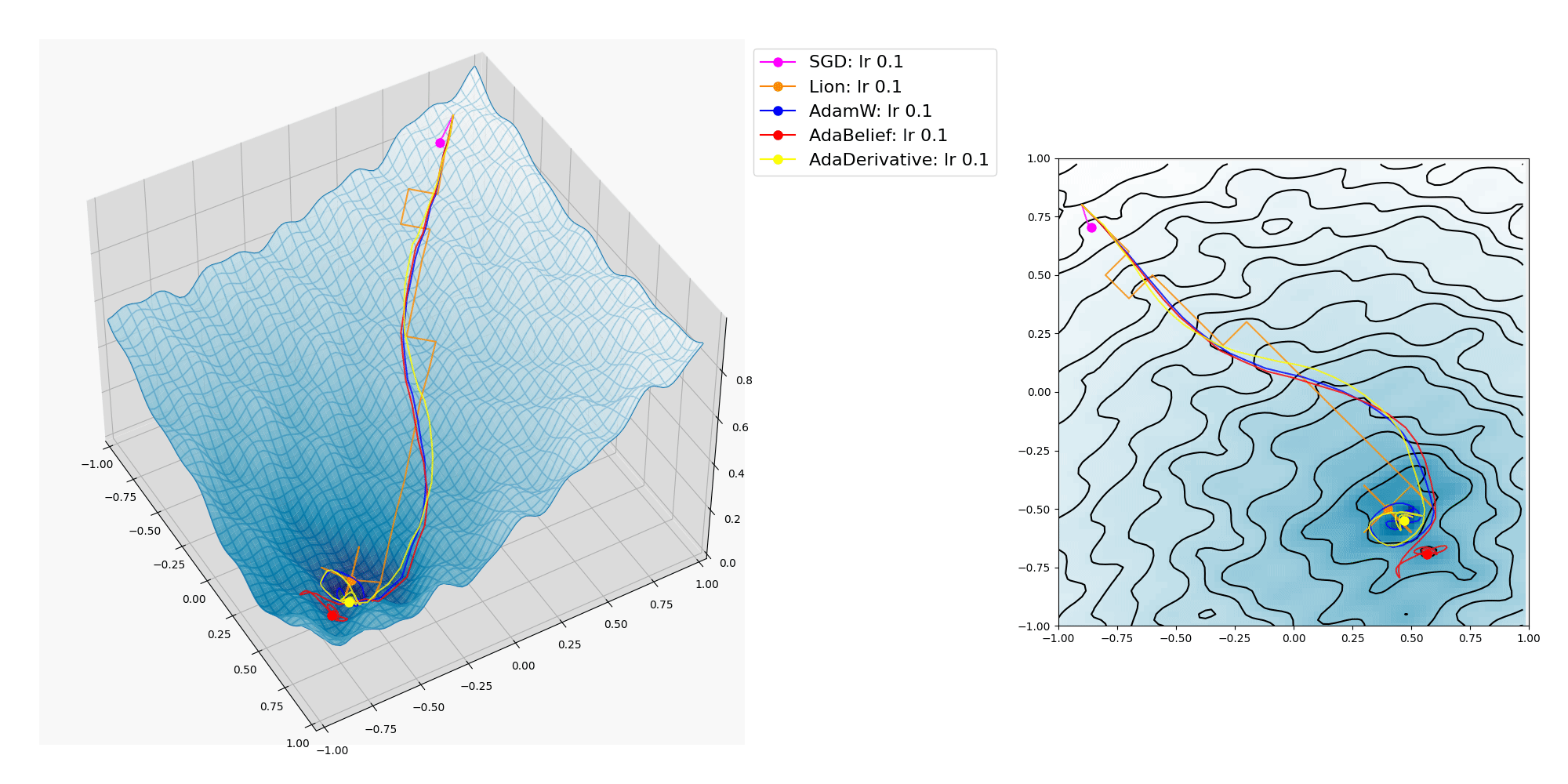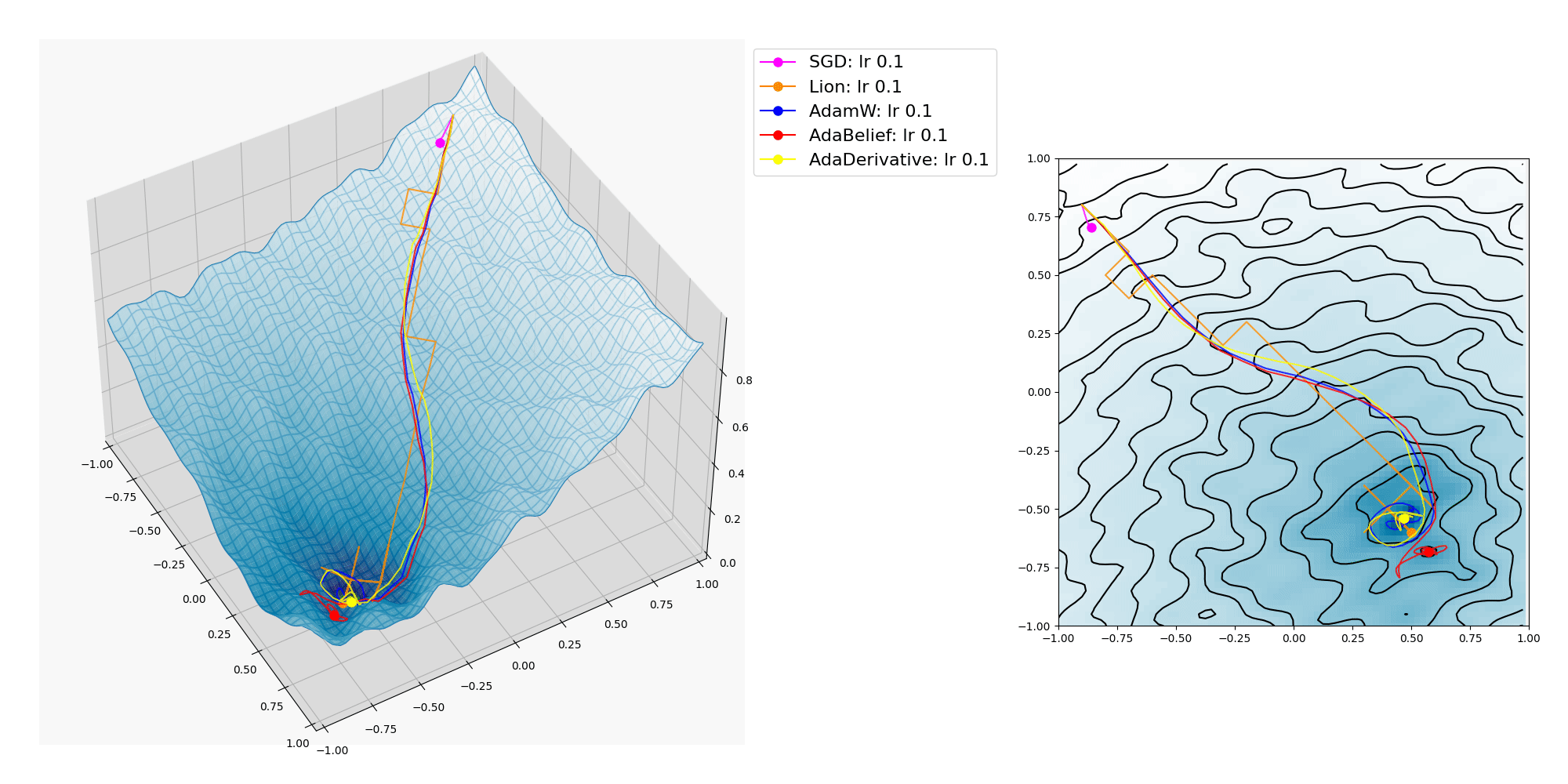
波面のうねりを細かくしたら AdaBelief も局所的最適解に捕われてしまいました。
AdaDerivative オプティマイザー
因みに AdaDerivative はそれについての論文を元に、GitHubにコードが掲載されていた AdaBeliefの、勾配のEMAと現在の勾配との差分を取るところを、現在の勾配と1ステップ前の勾配との差分を取るように書き換えて使用しております。
“AdaDerivative optimizer: Adapting step-sizes by the derivative term in past gradient information – ScienceDirect” のURL:
https://www.sciencedirect.com/science/article/abs/pii/S095219762200745X
AdaDerivativeはその挙動は優れているのですが、残念な事に前回の勾配の値を保存する必要が有り、保存する状態値がLionが1つ、AdamW、AdaBeliefが2つに対して、AdaDelivativeは3つとなり、メモリーの使用量が1.5倍になってしまいます。
なるべく大きなモデルを学習させたいのでメモリー使用量が多いのは短所と言えます。
サンプル コード
以下にオプティマイザーの振る舞いをプロットする為に書いたPythonスクリプトの拙いコードを掲載いたします。
また、GitHubにもプロット用のコードを掲載してあります。
https://github.com/ImpactCrater/OptimizerVisualizer/tree/main
#! /usr/bin/python3
# -*- coding: utf8 -*-
import os, time, random, re, glob
from os.path import expanduser
from pathlib import Path
import math
import random
import numpy
import torch
from torch.utils.data import DataLoader, Dataset
import torchvision
from torchvision import transforms, utils
import SGD
import Lion
import AdamW
import AdaDerivative
import AdaBelief
import AdaBC
import matplotlib
from matplotlib import pyplot
from matplotlib.colors import LogNorm
from matplotlib.animation import FuncAnimation
#python3 ~/Program/OptimizerVisualizer/optimizerVisualizer.py
# Mini Batch
miniBatchSize = 1
#Paths
# Home Path
homePath = expanduser("~")
plotImagePath = homePath + "/Program/OptimizerVisualizer/Plots"
objectiveFunctionNames = ['Rosenbrock', 'SixHumpCamel', 'Sphere', 'Rastrigin', 'Custom', 'Custom2', 'Custom3']
numberOfFrames = 100
pi = torch.tensor(math.pi)
e = torch.tensor(math.e)
deltaZ = 1e-5
def rosenbrockFunction(x, y):
scaleX = torch.tensor(2)
scaleY = torch.tensor(2)
shiftY = torch.tensor(1)
scaleZ = torch.tensor(2509) # Maxima: 2509.00000000, Minima: 0.00000000
x = x * scaleX
y = - y * scaleY + shiftY
a = 1
b = 100
z = a * (x - 1) ** 2 + b * (y - x ** 2) ** 2
z = z / scaleZ * (1 - deltaZ) + deltaZ
return z
def sixHumpCamelFunction(x, y):
scaleX = torch.tensor(2)
scaleY = torch.tensor(- 1)
rangeZ = 5.49558687 + 1.03008306 # Maximum: 5.49558687, Minimum: - 1.03008306
scaleZ = torch.tensor(rangeZ)
shiftZ = torch.tensor(1.03008306)
x = x * scaleX
y = y * scaleY
term1 = (4 - 2.1 * x ** 2 + (x ** 4) / 3) * x ** 2
term2 = x * y
term3 = (- 4 + 4 * y ** 2) * y ** 2
z = term1 + term2 + term3
z = (z + shiftZ) / scaleZ * (1 - deltaZ) + deltaZ
return z
def sphereFunction(x, y):
shiftY = torch.tensor(- 0.4)
rangeZ = 2.46000004 # Maxima: 2.46000004, Minima: 0.00000000
scaleZ = torch.tensor(rangeZ)
y = - y + shiftY
z = 0.5 * x ** 2 + y ** 2
z = z / scaleZ * (1 - deltaZ) + deltaZ
return z
def rastriginFunction(x, y):
scaleX = torch.tensor(5.12)
scaleY = torch.tensor(5.12)
rangeZ = 79.98309326 # Maximum: 79.98309326, Minimum: 0.00000000
scaleZ = torch.tensor(rangeZ)
x = x * scaleX
y = y * scaleY
a = 2
z = a + (x ** 2 - a * torch.cos(2 * pi * x)) + a + (y ** 2 - a * torch.cos(2 * pi * y))
z = z / scaleZ * (1 - deltaZ) + deltaZ
return z
def customFunction(x, y):
scaleX1 = torch.tensor(2)
scaleY1 = torch.tensor(- 1)
rangeZ1 = 5.49558687 + 1.03008306 # Maximum: 5.49558687, Minimum: - 1.03008306
scaleZ1 = torch.tensor(rangeZ1)
shiftZ1 = torch.tensor(1.03008306)
x1 = x * scaleX1
y1 = y * scaleY1
term1 = (4 - 2.1 * x1 ** 2 + (x1 ** 4) / 3) * x1 ** 2
term2 = x1 * y1
term3 = (- 4 + 4 * y1 ** 2) * y1 ** 2
z1= term1 + term2 + term3
z1 = (z1 + shiftZ1) / scaleZ1 * (1 - deltaZ) + deltaZ
shiftX2 = torch.tensor(- 1)
shiftY2 = torch.tensor(1)
rangeZ2 = 7.90062523 - 0.00062500 # Maximum: 7.90062523, Minimum: 0.00062500
scaleZ2 = torch.tensor(rangeZ2)
shiftZ2 = torch.tensor(- 0.00062500)
x2 = x + shiftX2
y2 = y + shiftY2
z2 = x2 ** 2 + y2 ** 2
z2 = (z2 + shiftZ2) / scaleZ2 * (1 - deltaZ) + deltaZ
rangeZ = 1.00000000 - 0.07055350 # Maximum: 1.00000000, Minimum: 0.07055350
scaleZ = torch.tensor(rangeZ)
shiftZ = torch.tensor(- 0.07055350)
z = 0.5 * z1 + 0.5 * z2
z = (z + shiftZ) / scaleZ * (1 - deltaZ) + deltaZ
return z
def custom2Function(x, y):
scaleX1 = torch.tensor(3)
scaleY1 = torch.tensor(3)
rangeZ1 = 6.80937624 + 7.99237823 # Maximum: 6.80937624, Minimum: -7.99237823
scaleZ1 = torch.tensor(rangeZ1)
shiftZ1 = torch.tensor(7.99237823)
x1 = x * scaleX1
y1 = y * scaleY1
term1 = x1 - torch.sin(2 * x1 + 3 * y1) - torch.cos(3 * x1 - 5 * y1)
term2 = y1 - torch.sin(x1 - 2 * y1) + torch.cos(x1 + 3 * y1)
z1 = term1 + term2
z1 = (z1 + shiftZ1) / scaleZ1 * (1 - deltaZ) + deltaZ
shiftX2 = torch.tensor(- 0.5)
shiftY2 = torch.tensor(0.5)
rangeZ2 = 1.48755252 # Maximum: 1.48755252, Minimum: 0.00000000
scaleZ2 = torch.tensor(rangeZ2)
x2 = x + shiftX2
y2 = y + shiftY2
z2 = torch.sqrt((x2 ** 2 + y2 ** 2) / 2)
z2 = z2 / scaleZ2 * (1 - deltaZ) + deltaZ
rangeZ = 0.90223962 - 0.16485822 # Maximum: 0.90223962, Minimum: 0.16485822
scaleZ = torch.tensor(rangeZ)
shiftZ = torch.tensor(- 0.16485822)
z = 0.3 * z1 + 0.7 * z2
z = (z + shiftZ) / scaleZ * (1 - deltaZ) + deltaZ
return z
def custom3Function(x, y):
scaleX1 = torch.tensor(6)
scaleY1 = torch.tensor(6)
rangeZ1 = 13.22151566 + 13.42661095 # Maximum: 13.22151566, Minimum: -13.42661095
scaleZ1 = torch.tensor(rangeZ1)
shiftZ1 = torch.tensor(13.42661095)
x1 = x * scaleX1
y1 = y * scaleY1
term1 = x1 - torch.sin(2 * x1 + 3 * y1) - torch.cos(3 * x1 - 5 * y1)
term2 = y1 - torch.sin(x1 - 2 * y1) + torch.cos(x1 + 3 * y1)
z1 = term1 + term2
z1 = (z1 + shiftZ1) / scaleZ1 * (1 - deltaZ) + deltaZ
shiftX2 = torch.tensor(- 0.5)
shiftY2 = torch.tensor(0.5)
rangeZ2 = 1.48755252 # Maximum: 1.48755252, Minimum: 0.00000000
scaleZ2 = torch.tensor(rangeZ2)
x2 = x + shiftX2
y2 = y + shiftY2
z2 = torch.sqrt((x2 ** 2 + y2 ** 2) / 2)
z2 = z2 / scaleZ2 * (1 - deltaZ) + deltaZ
rangeZ = 0.86382282 - 0.15205750 # Maximum: 0.86382282, Minimum: 0.15205750
scaleZ = torch.tensor(rangeZ)
shiftZ = torch.tensor(- 0.15205750)
z = 0.3 * z1 + 0.7 * z2
z = (z + shiftZ) / scaleZ * (1 - deltaZ) + deltaZ
return z
def objectiveFunction(objectiveFunctionName, x, y):
if objectiveFunctionName == 'Rosenbrock':
return rosenbrockFunction(x, y)
elif objectiveFunctionName == 'SixHumpCamel':
return sixHumpCamelFunction(x, y)
elif objectiveFunctionName == 'Sphere':
return sphereFunction(x, y)
elif objectiveFunctionName == 'Rastrigin':
return rastriginFunction(x, y)
elif objectiveFunctionName == 'Custom':
return customFunction(x, y)
elif objectiveFunctionName == 'Custom2':
return custom2Function(x, y)
elif objectiveFunctionName == 'Custom3':
return custom3Function(x, y)
print("Checking the existence of the directory to save plotted images.")
if os.path.isdir(plotImagePath):
print("Okay.")
else:
print("Making the directory.")
os.mkdir(plotImagePath)
print(plotImagePath + " has been created.")
optimizerDictionary = {'SGD': {}, 'Lion': {}, 'AdamW': {}, 'AdaBelief': {}, 'AdaDerivative': {}, 'AdaBC': {}}
optimizerDictionary['SGD']['color'] = 'magenta'
optimizerDictionary['Lion']['color'] = 'darkorange'
optimizerDictionary['AdamW']['color'] = 'blue'
optimizerDictionary['AdaBelief']['color'] = 'red'
optimizerDictionary['AdaDerivative']['color'] = 'yellow'
optimizerDictionary['AdaBC']['color'] = 'lawngreen'
for objectiveFunctionName in objectiveFunctionNames:
optimizerDictionary['SGD']['learningRate'] = 1e-1
optimizerDictionary['Lion']['learningRate'] = 1e-1
optimizerDictionary['AdamW']['learningRate'] = 1e-1
optimizerDictionary['AdaBelief']['learningRate'] = 1e-1
optimizerDictionary['AdaDerivative']['learningRate'] = 1e-1
optimizerDictionary['AdaBC']['learningRate'] = 1e-1
for key in optimizerDictionary:
if objectiveFunctionName == 'Rastrigin':
x = torch.tensor(- 0.7, requires_grad=True)
y = torch.tensor(0.8, requires_grad=True)
elif objectiveFunctionName == 'Custom3':
x = torch.tensor(- 0.9, requires_grad=True)
y = torch.tensor(0.8, requires_grad=True)
else:
x = torch.tensor(- 0.9, requires_grad=True)
y = torch.tensor(0.9, requires_grad=True)
optimizerDictionary[key]['parameters'] = [x, y]
optimizerDictionary[key]['xList'] = []
optimizerDictionary[key]['yList'] = []
optimizerDictionary[key]['zList'] = []
if key == 'SGD':
optimizerDictionary['SGD']['optimizer'] = SGD.SGD(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['SGD']['learningRate'], weight_decay=1e-16)
elif key == 'Lion':
optimizerDictionary['Lion']['optimizer'] = Lion.Lion(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['Lion']['learningRate'], betas=(0.9, 0.99), weight_decay=1e-16)
elif key == 'AdamW':
optimizerDictionary['AdamW']['optimizer'] = AdamW.AdamW(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['AdamW']['learningRate'], betas=(0.9, 0.999), eps=1e-16, weight_decay=1e-16)
elif key == 'AdaBelief':
optimizerDictionary['AdaBelief']['optimizer'] = AdaBelief.AdaBelief(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['AdaBelief']['learningRate'], betas=(0.9, 0.999), eps=1e-16, weight_decay=1e-16)
elif key == 'AdaDerivative':
optimizerDictionary['AdaDerivative']['optimizer'] = AdaDerivative.AdaDerivative(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['AdaDerivative']['learningRate'], betas=(0.9, 0.999), eps=1e-16, weight_decay=1e-16)
elif key == 'AdaBC':
optimizerDictionary['AdaBC']['optimizer'] = AdaBC.AdaBC(params=optimizerDictionary[key]['parameters'], lr=optimizerDictionary['AdaBC']['learningRate'], betas=(0.9, 0.999), eps=1e-16, weight_decay=1e-16)
X = numpy.arange(-1, 1, 0.025)
Y = numpy.arange(-1, 1, 0.025)
X, Y = numpy.meshgrid(X, Y)
X = torch.from_numpy(X.astype(numpy.float32)).clone()
Y = torch.from_numpy(Y.astype(numpy.float32)).clone()
Z = objectiveFunction(objectiveFunctionName, X, Y)
maximum = torch.max(Z)
print("Maximum: {:.8f}".format(maximum))
minimum = torch.min(Z)
print("Minimum: {:.8f}".format(minimum))
figure1 = pyplot.figure(figsize=(20, 10))
figure1.subplots_adjust(left=0., right=1., bottom=0., top=1., wspace=0.)
gridspec1 = figure1.add_gridspec(20, 40)
axis1 = figure1.add_subplot(gridspec1[1:19, 0:20], projection='3d', elev=45, azim=330, zorder=1, facecolor=(0.9, 0.9, 0.9, 0.25))
axis1.xaxis.pane.set_facecolor((0.75, 0.75, 0.75, 0.5))
axis1.yaxis.pane.set_facecolor((0.75, 0.75, 0.75, 0.5))
axis1.zaxis.pane.set_facecolor((0.75, 0.75, 0.75, 0.5))
axis2 = figure1.add_subplot(gridspec1[4:16, 27:39], facecolor=(0.9, 0.9, 0.9, 0.5))
#contour1.clabel(fmt='%1.1f', fontsize=8)
def update(i):
print('Step: {:3d}'.format(i + 1))
axis1.cla()
axis2.cla()
plotWireframe1 = axis1.plot_wireframe(X, Y, Z, rstride=2, cstride=2, zorder=1)
plotSurface1 = axis1.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='ocean', norm=LogNorm(), alpha=0.8, zorder=1)
plot2dContour = axis2.pcolormesh(X, Y, Z, cmap='ocean', norm=LogNorm(), zorder=1)
contour1 = axis2.contour(X, Y, Z, levels=16, colors=['black'])
for key in optimizerDictionary:
optimizerDictionary[key]['optimizer'].zero_grad()
outputs = objectiveFunction(objectiveFunctionName, optimizerDictionary[key]['parameters'][0], optimizerDictionary[key]['parameters'][1])
outputs.backward()
optimizerDictionary[key]['xList'].append(optimizerDictionary[key]['parameters'][0].item())
optimizerDictionary[key]['yList'].append(optimizerDictionary[key]['parameters'][1].item())
optimizerDictionary[key]['zList'].append(outputs.item())
optimizerDictionary[key]['optimizer'].step()
labelString = key + ': lr ' + str(optimizerDictionary[key]['learningRate'])
plot1 = axis1.plot(optimizerDictionary[key]['xList'], optimizerDictionary[key]['yList'], optimizerDictionary[key]['zList'], color=optimizerDictionary[key]['color'], marker='', linestyle='-', alpha=0.8, markersize=1, zorder=4)
plot1 = axis1.plot(optimizerDictionary[key]['xList'][-1], optimizerDictionary[key]['yList'][-1], optimizerDictionary[key]['zList'][-1], color=optimizerDictionary[key]['color'], marker='o', linestyle='-', alpha=1.0, markersize=8, zorder=4, label=labelString)
plotScatter1 = axis2.plot(optimizerDictionary[key]['xList'], optimizerDictionary[key]['yList'], color =optimizerDictionary[key]['color'], marker='', linestyle='-', alpha=0.8, markersize=1, zorder=2)
plotScatter1 = axis2.plot(optimizerDictionary[key]['xList'][-1], optimizerDictionary[key]['yList'][-1], color =optimizerDictionary[key]['color'], marker='o', linestyle='-', alpha=1.0, markersize=8, zorder=2)
#axis1.set_xlabel('x', fontsize=8)
#axis1.set_ylabel('y', fontsize=8)
#axis1.set_zlabel('z', fontsize=8)
axis1.set_xlim(- 1, 1)
axis1.set_ylim(- 1, 1)
axis2.set_xlim(- 1, 1)
axis2.set_ylim(- 1, 1)
axis1.legend(bbox_to_anchor=(1., 1.), loc='upper left', fontsize=16)
#pyplot.savefig(plotImagePath + '/{}_optim_{}.png'.format(objectiveFunctionName, key))
animation = FuncAnimation(fig=figure1, func=update, frames=numberOfFrames, interval=100, repeat=False)
animation.save(plotImagePath + '/Optimizers (' + objectiveFunctionName + ').gif')
記事やコードの内容に不備や誤りがあるかもしれませんのが、悪しからず。


コメント